Cho tứ giác ABCD, \(\widehat{A}=\widehat{C}=90^o\). Vẽ \(CH⊥AB\). Biết rằng đường chéo AC là đường phân giác của \(\widehat{A}\)và \(CH=6cm\). Tính diện tích của tứ giác ABCD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Bạn tham khảo lời giải tại đây:
Câu hỏi của Trần Huỳnh Tú Trinh - Toán lớp 9 | Học trực tuyến
Với TH $CH=a=6$ cm thì theo lời giải ta có $S_{ABCD}=a^2=36$ (cm vuông)

Lời giải:
Kẻ $CT\perp AD$
Vì $\widehat{A}=90^0$ mà $AC$ là tia phân giác của góc $A$ nên $\widehat{HAC}=\widehat{CAT}=45^0$
Tam giác vuông tại $H$ là $HAC$ có góc $\widehat{HAC}=45^0$ nên là tam giác vuông cân, suy ra CH=AH$
Tứ giác $HATC$ có 4 góc đều là góc vuông và 2 cạnh kề nhau $CH=AH$ nên $HATC$ là hình vuông
$\Rightarrow CT=CH$
Xét tam giác $TDC$ và $HBC$ có:
$\widehat{DTC}=\widehat{BHC}=90^0$
$\widehat{TCD}=\widehat{HCB}(=90^0-\widehat{HCD})$
$TC=HC$ (cmt)
$\Rightarrow \triangle TDC=\triangle HBC(g.c.g)$
$\Rightarrow S_{TDC}=S_{HBC}$
Do đó:
$S_{ABCD}=S_{HBC}+S_{HADC}=S_{TDC}+S_{HADC}=S_{HACT}=CH^2=a^2$
(đơn vị diện tích)
Vậy....

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

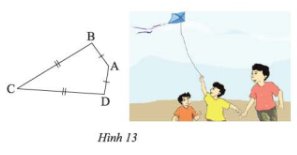
a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân



Vì AC là đường phân giác của góc A, suy ra đây là tính tình chất của hình vuông(mỗi đường chéo là đường phân giác 1 góc)
-> Tứ giác ABCD là hình vuông
Mà CH vuông góc với AB ->C trùng với B-> CB vuông góc với B
Theo đề, CH = 6 cm hay CB = 6 cm
-> Diện tích tứ giác ABCD là:
S(ABCD)= 6.6 =36(cm^2)
Vì AC là đường phân giác của góc A, nên:
\(\Rightarrow\)Tứ giác ABCD là hình vuông.
Mà CH vuông góc với AB:
\(\Rightarrow\)C trùng với B
\(\Rightarrow\)CB vuông góc với B
Theo đề bài, CH = 6cm hay CB = 6cm
\(\Rightarrow\)Diện tích tứ giác ABCD là:
S ( ABCD ) = 6.6 = 36 (cm2)
Đáp số:....