Trên mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = - x + 6 và parabol (P): y = x².
a, Tìm tọa độ các giao điểm của (d) và (P).
b, Gọi A, B là giao điểm của (d) và (P). Tính diện tích tam giác OAB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)

a: 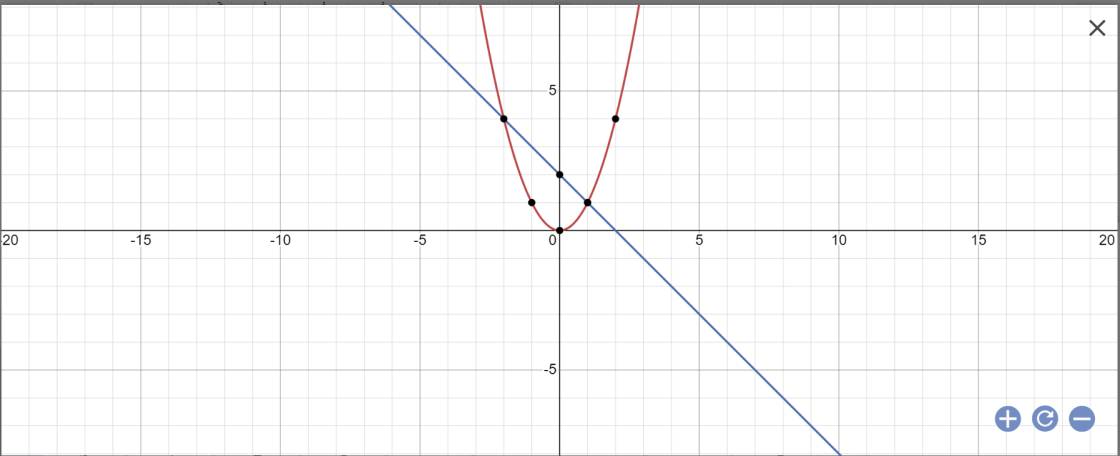
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a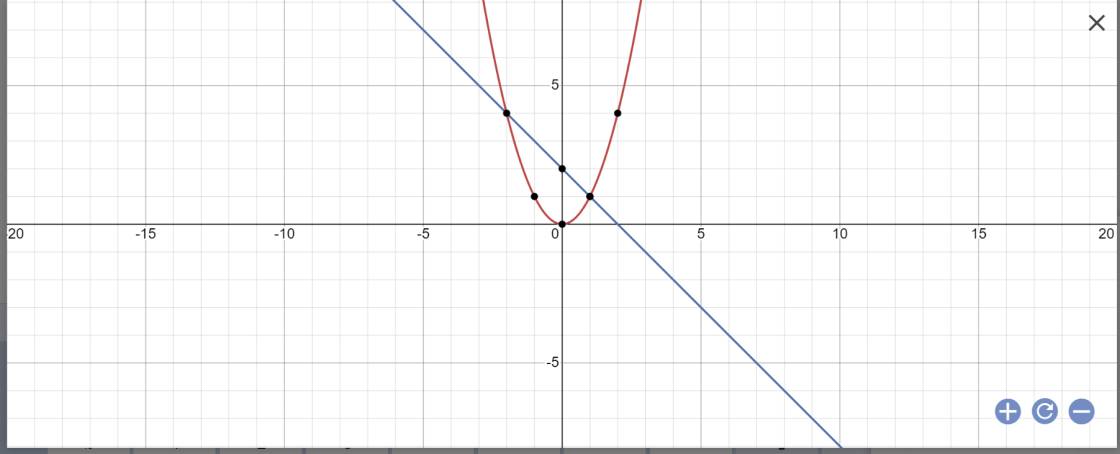
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a: Phương trình hoành độ giao điểm là:
\(x^2=-x+2\)
=>\(x^2+x-2=0\)
=>(x+2)(x-1)=0
=>\(\left[{}\begin{matrix}x+2=0\\x-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
Thay x=-2 vào (P), ta được:
\(y=\left(-2\right)^2=4\)
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
b: A(-2;4); B(1;1)
\(OA=\sqrt{\left(-2-0\right)^2+\left(4-0\right)^2}=2\sqrt{5}\)
\(OB=\sqrt{\left(1-0\right)^2+\left(1-0\right)^2}=\sqrt{2}\)
\(AB=\sqrt{\left(1+2\right)^2+\left(1-4\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)
Vì \(OB^2+AB^2=OA^2\)
nên ΔOAB vuông tại B
=>\(S_{OAB}=\dfrac{1}{2}\cdot BO\cdot BA=\dfrac{1}{2}\cdot3\sqrt{2}\cdot\sqrt{2}=3\)

b) Phương trình hoành độ giao điểm là:
\(-2x^2=x-3\)
\(\Leftrightarrow-2x^2-x+3=0\)
\(\Leftrightarrow-2x^2+2x-3x+3=0\)
\(\Leftrightarrow-2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số y=x-3, ta được:
y=1-3=-2
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=x-3, ta được:
\(x=-\dfrac{3}{2}-3=-\dfrac{9}{2}\)
Vậy: M(1;-2) và \(N\left(-\dfrac{3}{2};-\dfrac{9}{2}\right)\)

a: 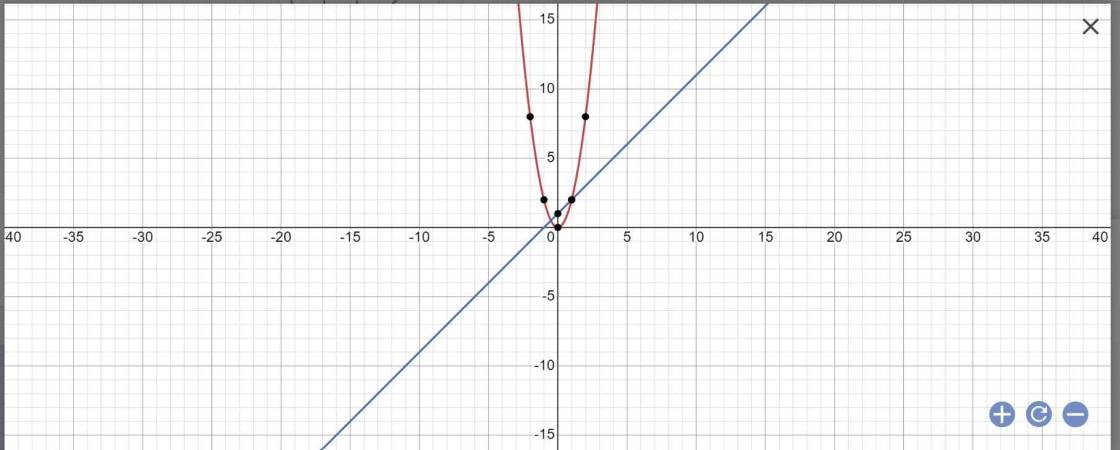
b: PTHĐGĐ là:
2x^2=x+1
=>2x^2-x-1=0
=>2x^2-2x+x-1=0
=>(X-1)(2x+1)=0
=>x=-1/2 hoặc x=1
=>y=2*1/4=1/2 hoặc y=2
câu a: phương trình hoành độ giao điểm x^2= -x+6 <=> x^2 +x-6=0 <=> x=2 và x=-3
toạ độ các giao điểm là A(2;4) và B(-3;9)
câu b: bạn phải vẽ hình ra ta sẽ thấy tam giác OAB là tam giác vuông với 2 cạnh OA và OB là 2 cạnh góc vuông, dựa vào hình vẽ sẽ tính được
tính OA=\(\sqrt{\left(2^2+4^2\right)}\)=\(\sqrt{20}\) và OB=\(\sqrt{\left(\left(-3\right)^2+9^2\right)}\)= \(\sqrt{90}\) sau đó tính diện tích tam giác OAB
S=\(\frac{1}{2}OA\cdot OB=\frac{1}{2}\sqrt{20}\cdot\sqrt{90}\)=\(3\sqrt{50}\)
ngô thị loan tại sao lại có thể nhìn hình để kết luận là tam giác vuông liền được ? mình vẽ đồ thị ra thi có phải tam giác vuông đâu, dùng Pytago thử lại cũng sai ??