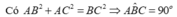Cho tam giác ABC có diện tích bằng 1.Hai học sinh chơi 1 trò chơi như sau:người thứ nhất chọn 1 điểm X trên cạnh BC,người thứ hai chọn một điểm Y trên cạnh BC và người thứ nhất tiếp tục chọn 1 điểm Z trên cạnh CA.Mục đích của người thứ nhất là làm cho tam giác XYZ có diện tích lớn nhất.Mục đích của người thứ hai là làm cho diện tích tam giác XYZ nhỏ nhất có thể được.Hỏi người thứ nhất có thể làm cho diện tích tam giác XYZ đạt đươch giá trị lớn nhất là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, k;
cin >> n >> k;
int ai[n];
for (int i = 0; i < n; i++) {
cin >> ai[i];
}
vector<int> pairs(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) continue;
if (ai[i] + ai[j] == k) {
pairs.push_back(make_pair(i, j));
}
}
}
sort(pairs.begin(), pairs.end());
int count = 0;
pairs.erase(pairs.begin(), pairs.end());
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (pairs[i].first == i && pairs[i].second == j) {
count++;
break;
}
}
if (count == n) {
break;
}
if (pairs[i].second == j) {
while (pairs[i].first != i) {
i++;
count++;
pairs.erase(pairs.begin() + i);
for (int j = 0; j < n; j++) {
if (ai[j] + ai[i] == k) {
pairs.push_back(make_pair(j, i+1));
break;
}
}
for (int j = 1;; j++) {
int count_n = 0, count_s = 0;
for (int i = j-1; i >= 0; i--) {
if (pairs[i].second == j) {
j++;
count_n++;
pairs.erase(pairs.begin() + i + 1);
pairs.er

Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
| Raashan |
Sylvia |
Ted |
| 1 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
1 |
0 |
| 2 |
0 |
1 |
| 1 |
2 |
0 |
| 0 |
2 |
1 |
| 1 |
0 |
2 |
| 0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là Raashan → Sylvia → Ted Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có 1 4 cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan ⇆ Sylvia và Ted không nhận được tiền.
Raashan → Sylvia → Ted.
- Raashan → Ted → Sylvia.
- Sylvia → Raashan → Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ 1 4
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
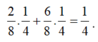

ngọc anh , tớ cũng muốn giúp cậu lắm nhưng tớ ko bít làm đành chịu thôi

Để tìm chiến thuật chơi để An là người thắng cuộc, ta cần xem xét các trường hợp có thể xảy ra.
Trong trường hợp này, số viên kẹo trong hai túi là 18 và 21. Ta có thể tạo bảng để phân tích các trường hợp:
| Lượt chơi | Túi 1 (18 viên) | Túi 2 (21 viên) |
|-----------|----------------|----------------|
| 1 | 17 | 20 |
| 2 | 16 | 19 |
| 3 | 15 | 18 |
| 4 | 14 | 17 |
| 5 | 13 | 16 |
| 6 | 12 | 15 |
| 7 | 11 | 14 |
| 8 | 10 | 13 |
| 9 | 9 | 12 |
| 10 | 8 | 11 |
| 11 | 7 | 10 |
| 12 | 6 | 9 |
| 13 | 5 | 8 |
| 14 | 4 | 7 |
| 15 | 3 | 6 |
| 16 | 2 | 5 |
| 17 | 1 | 4 |
| 18 | 0 | 3 |
Dựa vào bảng trên, ta nhận thấy rằng nếu An chơi một cách thông minh, an sẽ luôn giữ số viên kẹo trong hai túi ở cùng một mức. Điều này đảm bảo rằng Bình sẽ không thể lấy hết kẹo từ một túi nào đó và An sẽ luôn có cơ hội lấy kẹo từ túi còn lại.
Vì vậy, chiến thuật chơi của An là giữ số viên kẹo trong hai túi ở cùng mức. Khi Bình lấy đi một viên kẹo từ một túi, An sẽ lấy đi một viên kẹo từ túi còn lại để duy trì số viên kẹo ở cùng mức.
Với chiến thuật này, An sẽ luôn là người thắng cuộc vì An có thể điều khiển trò chơi sao cho Bình không thể lấy hết kẹo từ một túi nào đó.

a) *Bình đã chơi như sau:
+) TH1: Minh viết trước
=> Bình luôn viết các số là bội của 4
+) TH2: Minh viết sau
=> Bình viết số 0 đầu tiên và các số sau là bội của 4
*Minh có thể thắng Bình khi Minh biết quy luật và Minh đi trước
b) Đề xuất luật chơi mới:
Người chơi thứ nhất sẽ viết một số tự nhiên không lớn hơn 3. Sau đó đến lượt người thứ hai viết rồi quay lại người thứ nhất và cứ thế tiếp tục, ... sao cho kể từ sau số viết đầu tiên, mỗi bạn viết một số lớn hơn số bạn mình vừa viết nhưng không lớn hơn quá 3 đơn vị. Ai viết được số 25 trước thì người đó thắng.