Một cây tre cao 9m bị gãy ngang thân,ngọn cây chạm đất cách góc 3m.Hỏi điểm gãy cách góc bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
0
HT
4
HT
2
9 tháng 6 2015
Gọi chiều dài phần còn lại là x (m)
=> phần gãy là 9 - x (m)
Áp dụng ĐL Pi - ta go ta có: x2 + 32 = (9 - x)2
=> x2 + 9 = (9 - x)(9 - x)
=> x2 + 9 = 81 - 18x + x2
=> 18x = 81 - 9 = 72 => x = 72 : 18 = 4 m
Vậy điểm gãy cách gốc 4 m
CM
25 tháng 4 2018
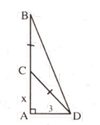
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
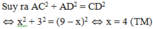
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 1
Giả sử gốc là điểm A, điểm gãy là B và điểm ngọn chạm đất là C, ta có tam giác ABC vuông tại A
Trong đó \(AC=3m\) ; \(AB+BC=9\left(m\right)\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2+3^2=\left(9-AB\right)^2\)
\(\Leftrightarrow9=81-18AB\)
\(\Rightarrow AB=4\left(m\right)\)
Vậy điểm gãy cách gốc 4m
NH
Một cây tre cao 9m bị gãy ngang thân, ngọn cây chạm đất cách gốc 3m. Hỏi độ dài từ điểm gãy tới gốc?
1
6 tháng 3 2016
gọi CDài phần còn lại là a (m)
=> phần gãy là 9-a (m)
áp dụng ĐL py-ta-go ta có: a2 + 32 =( 9-a)2
=> a2+9 = (9-a).(9-a)
a2+9 = 81 - 18a +a2
=> 18a = 81-9 = 72=> a= 72:18 = 4 m
vậy điểm gãy cách gốc 4 m
duyệt đi
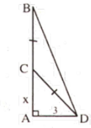
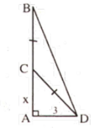
Gọi chiều dài phần còn lại là x (m)
=> phần gãy là 9 - x (m)
Áp dụng ĐL Pi - ta go ta có: x2 + 32 = (9 - x)2
=> x2 + 9 = (9 - x)(9 - x)
=> x2 + 9 = 81 - 18x + x2
=> 18x = 81 - 9 = 72 => x = 72 : 18 = 4 m
Vậy điểm gãy cách gốc 4 m