) Trong một hộp có 1 quả bóng ghi số 1, 2 quả bóng được ghi số 2,…, 20 quả bóng được ghi số 20. Ta lấy bóng từ hộp ra mà không nhìn, hỏi phải lấy ít nhất bao nhiêu quả để đảm bảo trong đó có 8 quả ghi số giống nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong trường hợp xấu nhất ta chọn phải tất cả các quả số 1, 2, ..., 9
và mỗi số từ 10 đến 100 mỗi số có 9 quả. Như vậy có tất cả 45+ 9×91 = 864
quả. Vậy phải lấy ít nhất 865 quả để đảm bảo có 10 quả cùng số.
Đáp số: 865.

Trong 30 lần Rô-bốt lấy bóng:
a) Bóng màu đỏ xuất hiện 10 lần; bóng màu xanh xuất hiện 12 lần; bóng màu vàng xuất hiện 8 lần.
b) Bóng màu xanh xuất hiện nhiều lần nhất, bóng màu vàng xuất hiện ít lần nhất.

Tham khảo:
a. Quả bóng Nam lấy ra có thể có màu: xanh, vàng và đỏ.
b.

c. Vẽ biểu đồ:
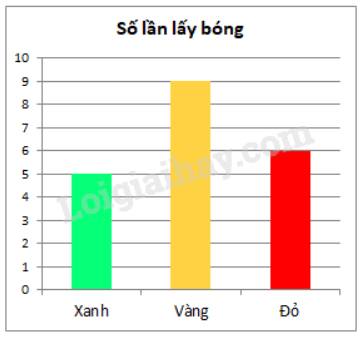
d. Xác suất thực nghiệm của các sự kiện Quả bóng lấy ra có màu xanh là: \(\frac{5}{{20}} = \frac{5}{{20}}.100\% = 25\% \)
Xác suất thực nghiệm của các sự kiện Quả bóng lấy ra có màu vàng là:
\(\frac{9}{{20}} = \frac{9}{{20}}.100\% = 45\% \)
Xác suất thực nghiệm của các sự kiện Quả bóng lấy ra có màu đỏ là:
\(\frac{6}{{20}} = \frac{6}{{20}}.100\% = 30\% \)

số bóng lấy ra ít nhất để có cả 4 màu, ta có 4t/hợp
1) 1+12+10+9= 32 (quả) vì chỉ cần 1 quả khác màu là 1 trong 8 quả bóng trắng
2) 8+ 1+10+9= 28( quả)
3) 8+12+1+9= 30( quả)
4) 8+ 12+ 10+9= 49( quả)
ta thấy 28 quả là số nhỏ nhất, vậy cần lấy 28 quả để đủ 4 màu

Trường hợp xấu nhất lấy ra tất cả đều là bóng đen và bóng xanh dương (35 + 32 = 67 quả) thì cần lấy ra ít nhất 68 quả bóng để chắc chắn rằng ta lấy được 1 quả bóng vàng

Trong trường hợp xấu nhất, ta lấy hết quả bóng đỏ, bóng xanh rồi mới lấy được quả bóng màu vàng
Khi đó số lần lấy để chắc chắn được 4 quả bóng màu vàng là:
10 + 14 + 4 = 28 (lần)

Vì 5 quả bóng có kích thước và khối lượng giống nhau nên 5 kết quả của phép thử có khả năng xảy ra bằng nhau.
- Biến cố \(A\) xảy ra khi ta lấy được quả bóng có số 5 hoặc 13 nên có 2 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{2}{5}\).
- Vì không có quả bóng nào đánh số chia hết cho 3 nên số kết quả thuận lợi của biến cố \(B\) là 0. Xác suất của biến cố \(B\) là
\(P\left( B \right) = \frac{0}{5} = 0\).
- Vì cả 5 quả bóng đều đánh số lớn hơn 4 nên số kết quả thuận lợi của biến cố \(C\) là 5. Xác suất của biến cố \(C\) là
\(P\left( C \right) = \frac{5}{5} = 1\).

10 quả bạn nha, vì nếu bạn lấy ra tối đa 5 quả xanh thì bạn cũng chắc chắn sẽ lấy được 5 quả đỏ, còn nếu bạn lấy được tối đa 7 qua đỏ thì chắc chắn bạn sẽ lấy được 3 quả xanh
chúc bạn học tốt nha
ủng hộ mk với nha


đề bài bị sao z, mà bn dùng nguyên lý dirichlet là đc
Trong trường hợp xấu nhất ta chọn phải tất cả các quả số 1, 2, ..., 7
và mỗi số từ 8 đến 20 mỗi số có 7 quả. Như vậy có tất cả 28+ 7×13 = 119
quả. Vậy phải lấy ít nhất 119 quả để đảm bảo có 8 quả cùng số.
Đáp số: 119