Tính tổng sau
S =(_1) +2 +(_3) + 4 +(_5) + ...... +(_2007) + 2008 + (_2009) + 2010
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
a) \(log_69+log_64=log_636=2\)
b) \(log_52-log_550=log_5\left(2:50\right)=-2\)
c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)
LH
20 tháng 4 2017
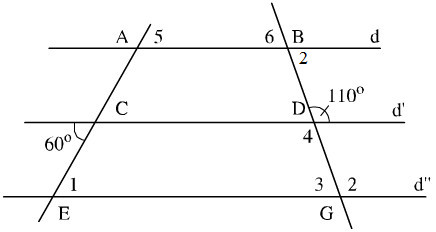
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
20 tháng 4 2017
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2
TH
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
\(1-3+\left(-2\right)-5+1-6+\left(-1\right)-5< x< \left(-3\right)-4+2-7+\left(-1\right)-4+3-5+5-7\)
\(\Rightarrow1-3-2-5+1-6-1-5< x< -3-4+2-7-1-4+3-5+5-7\)
\(\Rightarrow-9-6< x< -5-12-4\)
\(\Rightarrow-15< x< -21\)
Vậy không có x thỏa mãn
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
N
1
4 tháng 3 2015
A = [2 + (-3)] + [4 + (-5)] +.....+ [2008 + (-2009)] + [2010 + (-2011)]
= (-1) + (-1) +.....+ (-1) + (-1) (Có 2010 :2 = 1005 số -1)
= 1005. (-1) = -1005
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
a) \(log_3\sqrt[3]{3}=\dfrac{1}{2}\)
b) \(log_{\dfrac{1}{2}}8=-3\)
c) \(\left(\dfrac{1}{25}\right)^{log_54}=\dfrac{1}{16}\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
a) \(log_29\cdot log_34=4\)
b) \(log_{25}\cdot\dfrac{1}{\sqrt{5}}=-\dfrac{1}{4}\)
c) \(log_23\cdot log_9\sqrt{5}\cdot log_54=\dfrac{1}{2}\)
Ta có : S = (-1)+2+(-3)+4+(-5)+......+(-2007)+2008+(-2009)+2010
S = [(-1)+2]+[(-3)+4]+[(-5)+6]+......+[(-2007)+2008]+[(-2009)+2010]
S = 1 + 1 + 1 + ...... + 1 + 1 = 1 x 1005 ( vì có 2010 số hạng mà nhóm 2 số thì số nhóm phải là 2010 : 2 = 1005 )
S = 1005
Vậy S = 1005
Nhớ kick cho mình nha !