Hình chữ nhật ABCD có AC và BD cắt nhau tại O. Nếu BA = BC thì số đo của góc COD là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 8 2023
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AB//CD
=>góc OAB=góc OCD
mà góc OAB=góc ODC
nên góc ODC=góc OCD
=>OC=OD
=>AC=BD
Xét hình bình hành ABCD có AC=BD
nên ABCD là hình chữ nhật
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
a) Các cạnh đối diện của hình chữ nhật bằng nhau (AB = CD = 4,5 cm, BC = AD = 2,5 cm).
Các góc của hình chữ nhật đều bằng nhau và bằng \( 90^0\)
b) AB và CD song song với nhau.
AD và BC song song với nhau.
c) AC và BD bằng nhau (cùng bằng 5,1 cm).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
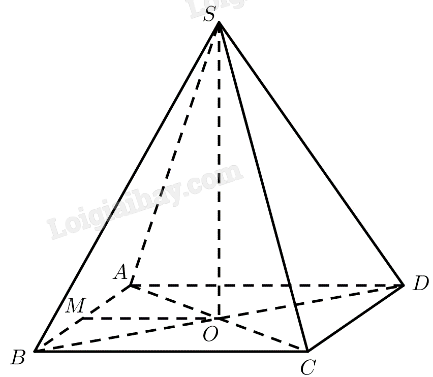
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)
\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)
b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)
\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)
Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)
\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)
\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)
\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).
PN
30 tháng 11 2015
A B C D O
Ta có:
ABCD là hình thoi nên AB = BC = CD = DA ( = CA = 4 cm)
Do đó: tam giác ABC là tam giác đều ( do AB = BC = CA ( = 4 cm))
Suy ra, góc B = 60o
Mà góc B và góc D là hai góc đối nhau nên theo tính chất hình thoi, góc D = 60o
------------------------------------
Theo tính chất hình thoi, 2 đường chéo vuông góc với nhau nên AC vuông góc với BD tại O
Tam giác đều ABC có OB là đường cao nên cũng là đường trung tuyến
Do đó: \(OA=OC=\frac{1}{2}.AC=\frac{1}{2}.4=2\) (cm)
Áp đụng định lý Py-ta-go vào tam giác OAB, ta được:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow\) \(OB^2=AB^2-OA^2=4^2-2^2=16-4=12\)
\(\Rightarrow\) \(OB=\sqrt{12}\) (cm)
Góc COD có số đo là 900
Vì theo t/c của hình chữ nhật thì giao điểm của hai đường chéo cắt nhau tại TĐ của mỗi đường
Suy ra :OB=OD
Mà BA=OB=OD
Suy ra: Góc COD=600 vì tam giác ấy đều