Bài 1: (2,0 điểm) Thực hiện các phép tính sau:
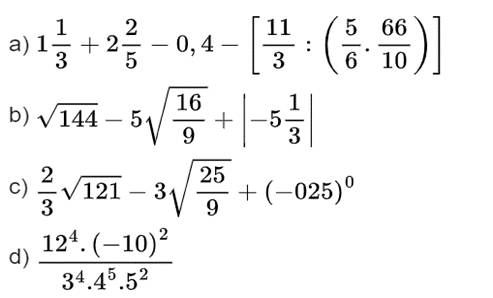
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)

a: \(=9-4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=9-4=5\)
b: \(=\sqrt{5}-2-\dfrac{1}{2}\cdot2\sqrt{5}=-2\)

a) (-124) + 24 = -100
b) 37. 78 + 37. 22
= 37 . ( 78 + 22 )
= 37 . 100
= 3700


Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{c-b}{4-3}=10\)
Do đó: a=60; b=30; c=40

Bài 1:
\(a.8,32+14,76+5,24=8,32+\left(14,76+5,24\right)\)
\(=8,32+20=28,32\)
\(b,16,88+9,76+3,12=\left(16,88+3,12\right)+9,76\)
\(=20+9,76=29,76\)
\(c,\left(\dfrac{2}{5}+\dfrac{7}{9}\right)+\dfrac{3}{5}=\left(\dfrac{2}{5}+\dfrac{3}{5}\right)+\dfrac{7}{9}\)
\(=1+\dfrac{7}{9}=\dfrac{16}{9}\)
\(d,\dfrac{19}{11}+\left(\dfrac{8}{13}+\dfrac{3}{11}\right)\)
\(=\left(\dfrac{19}{11}+\dfrac{3}{11}\right)+\dfrac{8}{13}=\dfrac{22}{11}+\dfrac{8}{13}\)
\(=2+\dfrac{8}{13}=\dfrac{34}{13}\)

Bài 1:
b: \(=\dfrac{x+3-4-x}{x-2}=\dfrac{-1}{x-2}\)
Bài 2:
a: \(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}\)
\(=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)
d: \(=\dfrac{3}{2x^2y}+\dfrac{5}{xy^2}+\dfrac{x}{y^3}\)
\(=\dfrac{3y^2+10xy+2x^3}{2x^2y^3}\)
e: \(=\dfrac{x^2+2xy+x^2-2xy-4xy}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2x^2-4xy}{\left(x+2y\right)\cdot\left(x-2y\right)}=\dfrac{2x}{x+2y}\)