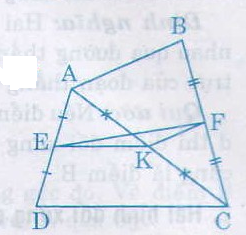
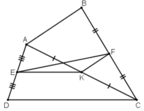
Cho tứ giác ABCD. Gọi E, F, K lần lượt là trung điểm của AD, BC, AC.
Vẽ hình dùm mik nha m.n
a) So sánh độ dài các đoạn thẳng EK và CD, KF và AB
b) Chứng minh : EF< AB+CD phần 2 ( phân số á mọi người)
c) Khi EF< AB+CD phần 2 ( phân số á mọi người) thì tứ giác ABCD là hình gì
mik đag cần gấp

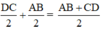
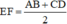 ⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)
⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)