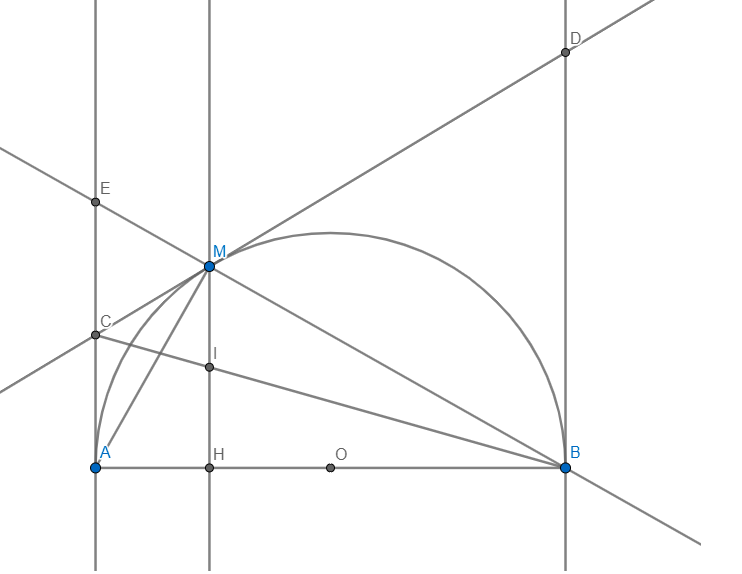
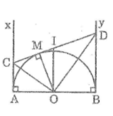
Cho nửa đường tròn tâm O, đường kính AB. Vẽ 2 tiếp tuyến Ax; By của nửa (O). Gọi C là điểm trên nửa (O) sao cho AC > BC. Tiếp tuyến tại C của nửa (O) cắt Ax; By lần lượt tại D; E.
a) Chứng minh: Tam giác ABC vuông và AD + BE = ED.
b) Chứng minh: 4 điểm A; D; C; O cùng thuộc 1 đường tròn và gócADO = gócCAB.
c) DB cắt nửa (O) tại F và cắt AE tại I. Tia CI cắt AB tại K. Chứng minh: IC = IK.
d) Tia AF cắt tia BE tại N, gọi M là trung điểm của BN. Chứng minh: 3 điểm A; C; M thẳng hàng.

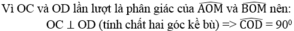
a)
► Tính chất của hai tiếp tuyến cùng xuất phát từ một điểm, ta có:
AC = CM ; BD = MD
=> AC + BD = CM + MD = CD
► Câu trên có thể cm trực tiếp bằng cách nối OC => hai tgiác ACO và MCO bằng nhau (vì tgiác vuông, có chung cạnh huyền, OA=OM=R)
=> OC là tia phân giác của góc AO^M
tương tự: OD cúng là phân giác cua góc BO^M
AO^C + CO^M + DO^M + DO^B = 180o
=> 2.CO^M + 2DO^M = 180o
=> CO^M + DO^M = CO^D = 90o
► tgiác COD vuông có OM là đường cao, hệ thức lượng:
CM.MD = OM²
=> AC.BD = R² (cm trên: AC=CM; BD=MD; OM=R)
► ad toilet với chú ý AC//BD
NC/NB = AC/BD = CM/MD
định lí đảo talet => MN//AC
► có: MN//AC//BD => hai tgiác CBD và CNM đồng dạng
=> CD/CM = DB/MN
=> CD.MN = CM.DB
► gọi K là trung điểm CD
do tgiác OCD vuông tại O => K là tâm đường tròn ngoại tiếp tgíc OCD
OK là đường trung bình của hình thang ABDC => OK//AC//BD
=> OK vuông góc AB tại O
=> AB là tiếp tuyến của đường tròn (OCD)
b)
► ta đã cm: AC+BD = CD
=> AC+BD nhỏ nhất khi CD nhỏ nhất
Có Ax //By, C thuộc Ax, D thuộc By
=> CD nhỏ nhất khi CD vuông góc vơi Ax và By
khi đó ta có ABDC là hình chữ nhật
=> M là điểm chính giữa của cung AB
► tứ giác ABDC thường là hình thang vuông, gọi diện tích là S
S = (1/2)AB.(AC+BD) = (1/2).AB.CD
vì AB cố định nên S nhỏ nhất khi CD nhỏ nhất
như câu trên có M là điểm chính giữa cung AB
c) tgiac OAM cân tại O, lại có OE là phân giác => OE vuông AM
tương tự OF vuông BM, mà CO^D= 90o
=> EOFM là hình chữ nhật
=> I là trung điểm EF cũng là trung điểm OM
=> OI = OM/2 = R/2
I di động nhưng luôn có OI = R/2 không đổi
=> I thuộc đường tròn cố định: tâm O bán kính r = R/2
** giới hạn: M chỉ di động trên nữa đường tròn (O,R) => I chỉ di động trên nữa đường tròn (O,r) nằm cùng phía với (O,R) so với AB
<< phần giới hạn là khuyến mãi thêm, vì đề chỉ yêu cầu cm I thuộc một đường tròn cố định, không phải tìm quỉ tích >>
d) dùng định lí Melanus là nhanh nhất: có ngay E,N,F thẳng hàng => EF/AB = ME.MA = MN/MJ = 1/2
=> MN = MJ/2 = NJ
Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath
Câu c) Đã có IK // AD thì ta vận dụng Ta let và thấy ngay :
\(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)