44.45+46.44+9.44
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
0
1 tháng 1 2017
\(\frac{1}{n^2\left(n+1\right)^2}=\frac{1}{2n+1}.\left[\frac{1}{n^2}-\frac{1}{\left(n+1\right)^2}\right]\)
\(A_n=\frac{2n+1}{n^2\left(n+1\right)^2}=\frac{1}{n^2}-\frac{1}{\left(n+1\right)^2}\\ \)
\(A=1-\frac{1}{\left(45\right)^2}\)
12 tháng 2 2017
Lời giải đây bn nhé :
\(\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+...+\frac{89}{\left(44.45\right)^2}\)
=\(\frac{3}{1.4}+\frac{5}{4.9}+...+\frac{89}{1936.2025}\)
=\(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{9}+...+\frac{1}{1936}-\frac{1}{2025}\)
=\(1-\frac{1}{2025}\)
=\(\frac{2024}{2025}\)
xong r nhé
6 tháng 5 2016
A = 1 - 1/2 + 1/2 - 1/3 + .... + 1/43 - 1/44 + 1/44 - 1/45 = 1 - 1/45 = 44/45
CX
6 tháng 5 2016
Theo mình nghĩ thì đề bải phải là 1/2.3 chứ không phải là 1/1.3
k nha
TG
30 tháng 11 2016
Khi dời dấu phẩy của một số thập phân sang bên trái 1 hàng thì số đó bằng \(\frac{1}{10}\)số cũ và số đó bé hơn số cũ 10 - 1 = 9 lần
Số lớn - \(\frac{1}{10}\)số bé = 44,45
Số lớn + số bé = 58,2 -> số lớn = 58,2 - số bé
58,2 - số bé - \(\frac{1}{10}\)số bé = 44,45
58,2 - \(\frac{11}{10}\)số bé = 44,45
58,2 - 44,45 = \(\frac{11}{10}\)số bé
số bé = 13,75 : \(\frac{11}{10}\)
Số bé là : 12,5
Số lớn là :
58,2 - 12,,5 = 45,7
Thử lại : 45,7 - 12,5 x \(\frac{1}{10}\)= 44,45 -> đúng
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
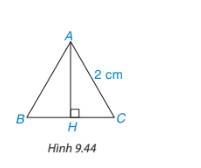
Vì tam giác ABC là tam giác đều, \(AH \bot BC\) nên H là trung điểm của BC suy ra
\(HB = HC = \frac{{BC}}{2} = \frac{2}{2} = 1\)(cm)
Áp đụng định lí Pythagore trong tam giác AHC ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2} \Rightarrow A{H^2} = A{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow AH = \sqrt 3 \approx 1,73(cm)\end{array}\)
Vậy chiều cao của tam giác đều là 1,73cm.
HP
24 tháng 12 2016
1,tổng quát: (2k+1)/[k(k+1)^2]
=(2k+1)/k^2(k+1)^2=[(k+1)^^2-k^2]/k^2(k+1)^2=1/k^2-1/(k+1)^2
áp dụng vào ,kết quả =2024/2025
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
- Xét tam giác ABE vuông tại B, có
\(A{{\rm{E}}^2} = A{B^2} + B{E^2} = {5^2} + {3^2} = 34 \Rightarrow A{\rm{E}} = \sqrt {34} cm\)
=> Chú chó có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây
- Xét tam giác ADF vuông tại D, có
\({\rm{A}}{{\rm{F}}^2} = A{{\rm{D}}^2} + D{F^2} = {5^2} + {4^2} = 41 \Rightarrow A{\rm{E}} = \sqrt {41} cm\)
=> Chú chó không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây
- Xét tam giác ADC vuông tại D, có
\(A{C^2} = A{{\rm{D}}^2} + D{C^2} = {5^2} + {5^2} = 50 \Rightarrow A{\rm{E}} = 5\sqrt 2 cm\)
=> Chú chó không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây
Vậy chú chó không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E
KK
8 tháng 2 2017
\(C1:\)\(S\)\(=225\)\(cm^2\)\(\Leftrightarrow\)\(S=\left(4x-1\right)^2\)
\(\Rightarrow\left(4x-1\right)^2=225\)
\(\Rightarrow\left(4x-1\right)^2=15^2\Rightarrow4x-1=15\)
\(\Rightarrow4x=16\)
\(\Rightarrow x=4\)
44.45+46.44+9.44
= 44 . ( 45 + 46 + 9 )
= 44. 100
= 4400
44 .( 45 + 46 + 9)
= 44.100
= 4400