Tìm các số nguyên dương x, y thỏa mãn x3 -xy=y3 +25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TV
0

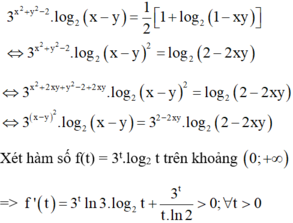

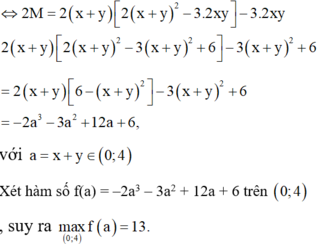
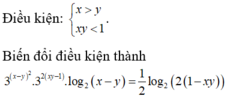
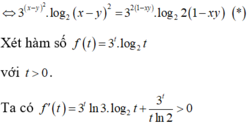

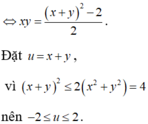
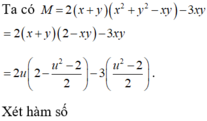
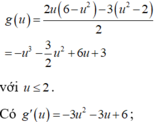
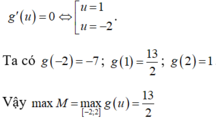
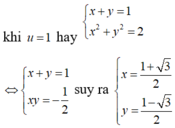
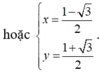
\(x^3-xy=y^3+25\)
Ta có :
\(x^3-y^3=xy+25\)
\(\Leftrightarrow\left(x-y\right)^3+3xy\left(x-y\right)=xy+25\)
Đặt \(x-y=a;\)\(xy=b\)Ta có :
\(a^3+3ab=b+25\)
\(\Leftrightarrow a^3-25=-b\left(3a-1\right)\)
\(\Leftrightarrow27\left(a^3-25\right)⋮3a-1\)
\(\Leftrightarrow27a^3-1-674⋮3a-1\)
Do \(27a^3-1⋮3a-1\Rightarrow674⋮3a-1\)
mà \(674=2.337\)
Nên \(3a-1\in\left\{\pm1;\pm2;\pm337;\pm674\right\}\)
Do \(3a-1⋮3\)( Dư 2 )
Nên \(3a-1\in\left\{-1;2;-337;674\right\}\)
\(\Rightarrow a\in\left\{0;1;-112;225\right\}\)
Ta có : \(b=a^3-25̸\)\(1-3a\)
\(\left(a,b\right)=\left(0,-25\right);\left(1,12\right);\left(-112;4169\right);\left(225;-16900\right)\)
Vì \(\left(x-y\right)^2+4xy\ge0\Rightarrow a^2+4b\ge0\)Vì vậy chỉ có a = 1 , y = 12 . \(\Rightarrow x-y=1;xy=12\)
Vậy \(\left(x,y\right)=\left(4,3\right);\left(-3,-4\right)\)