Tìm đa thức dư của phép chia đa thức x300 - 3x299 + 5 cho x2 - 4x +3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có đa thức x 2 + 3 x + 2 5 + x 2 - 4 x - 4 5 - 1 chưa (x + 1) nên phần dư là một hằng số
Gọi thương là Q(x) và dư r. Khi đó với mọi x ta có
x 2 + 3 x + 2 5 + x 2 - 4 x - 4 5 - 1 = Q(x)(x + 1) + r (1)
Thay x = -1 vào (1) ta được
( ( - 1 ) 2 + 3 . ( - 1 ) + 2 ) 5 + ( ( - 1 ) 2 – 4 ( - 1 ) – 4 ) 5 – 1 = Q(x).(-1 + 1) + r
r = 0 5 + 1 5 – 1 ó r = 0
vậy phần dư của phép chia là r = 0.
đáp án cần chọn là: C

Ta có phép chia
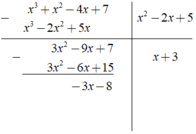
Dựa vào kết quả của phép chia trên, ta có đa thức dư là - 3x - 8.
Chọn đáp án B.

Ta có phép chia
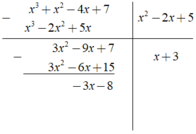
Dựa vào kết quả của phép chia trên,, ta có đa thức dư là - 3x - 8.
Chọn đáp án B.

Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)



Ta có

Vì phần dư R = 0 nên Phép chia đa thức (2 x 3 – 26x – 24) cho đa thức x 2 + 4x + 3 là phép chia hết.
Do đó (I) đúng.
Lại có
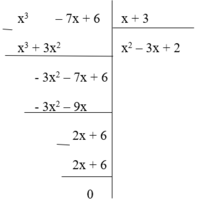
Nhận thấy phần dư R = 0 nên phép chia đa thức ( x 3 – 7x + 6) cho đa thức x + 3 là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: A

Lời giải:
Ta có:
$2x^4-3x^3-3x-2=2x^2(x^2-1)-3x(x^2-1)+2x^2-6x-2$
$=(2x^2-3x)(x^2-1)+2(x^2-1)-6x$
$=(2x^2-3x+2)(x^2-1)-6x$
Vậy $2x^4-3x^3-3x-2$ chia $x^2-1$ dư $-6x$
Không có đáp án nào đúng
