Tìm điều kiện để biểu thức sau xác định :
\(\sqrt{x^2-6x+9}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ : \(-x^2+6x-9\ge0\)
\(\Leftrightarrow\)\(-\left(-x^2+6x-9\right)\le0\)
\(\Leftrightarrow\)\(x^2-6x+9\le0\)
\(\Leftrightarrow\)\(\left(x-3\right)^2\le0\)
Mà \(\left(x-3\right)\ge0\)
Suy ra : \(\left(x-3\right)^2=0\)
\(\Leftrightarrow\)\(x-3=0\)
\(\Leftrightarrow\)\(x=3\)
Chưa học nên sai thì thôi nhé =.="
Chúc bạn học tốt ~

a: ĐKXĐ: \(-\dfrac{\sqrt{6}}{2}\le x\le\dfrac{\sqrt{6}}{2}\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)
c: ĐKXĐ: \(-\sqrt{5}< x< \sqrt{5}\)
d: ĐKXĐ: \(x\le\sqrt[3]{-5}\)

\(B=\sqrt{x^2+8x+14}+\sqrt{9-x^2}\)
ĐKXĐ :
\(\hept{\begin{cases}x^2+8x+14\ge0\\9-x^2\ge0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge-4-\sqrt{2}\\x\le3\end{cases}}\)
\(\Leftrightarrow-4-\sqrt{2}\le x\le3\)

a) x ≠ 0 , x ≠ − 2
b) Ta có D = x 2 - 2x - 2.
c) Chú ý D = - x 2 - 2x - 2 = - ( x + 1 ) 2 - 1 ≤ -1. Từ đó tìm được giá trị lớn nhất của D = -1 khi x = -1.

a) \(\sqrt{3x-4}\) xác định \(\Leftrightarrow3x-4\ge0\Leftrightarrow3x\ge4\Leftrightarrow x\ge\dfrac{4}{3}\)
b) \(\dfrac{1}{\sqrt{x-4}}\) xác định \(\Leftrightarrow x-4>0\Leftrightarrow x>4\)

Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
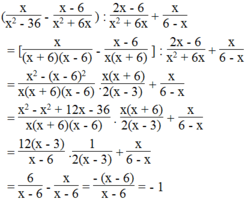
Vậy biểu thức không phụ thuộc vào biến x.

đkxđ:
\(x^2-4x+3\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x-3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x-3\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
Vậy đkxđ của biểu thức là \(\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
mik cũng ko chắc đâu nếu sai thì thôi nhé:
ĐKXĐ : −x2+6x−9≥0−x2+6x−9≥0
⇔⇔−(−x2+6x−9)≤0−(−x2+6x−9)≤0
⇔⇔x2−6x+9≤0x2−6x+9≤0
⇔⇔(x−3)2≤0(x−3)2≤0
Mà (x−3)≥0(x−3)≥0
Suy ra : (x−3)2=0(x−3)2=0
⇔⇔x−3=0x−3=0
⇔⇔x=3
ĐKXĐ: \(^{x^2}\)- 6x + 9 ≥0 với mọi x