cHO TAM GIac AOB vuong tai O voi duong cao OM . CM AB.OM=OA.OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:
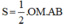
Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:
7 tháng 7 2022
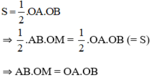
a: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
DO đó; ΔABD cân tại A
b: Ta có: \(\widehat{MCB}=90^0-\widehat{CDM}\)
\(\widehat{ACB}=90^0-\widehat{ABC}=90^0-\widehat{ADH}=90^0-\widehat{CDM}\)
=>góc MCB=góc ACB
hay CB là phân giác của góc AMC
c: Xét ΔCAQ có
CH là đường phân giác
CH là đường cao
Do đó: ΔCAQ cân tại C
3 tháng 2 2023
a: Xet ΔAHB vuôg tại H và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
b: Xét ΔAHB vuông tại H có HE là đường cao
nen AE*AB=AH^2
Xét ΔAHC vuông tạiH có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
c: góc MEB=góc AEF=góc AHF=góc MCF
Xét ΔMEB và ΔMCF có
góc MEB=góc MCF
góc M chung
=>ΔMEB đồng dạng với ΔMCF
=>ME/MC=MB/MF
=>ME/MB=MC/MF
=>ΔMEC đồng dạng với ΔMBF
=>góc MCE=góc MFB
TT
5 tháng 2 2020
Ta có : \(\Delta ABC\) cân tại \(A\) \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{ABC}=\widehat{ACB}\end{cases}}\) ( tính chất ) (1)
Lại có : \(\widehat{ABD}=\widehat{ABC}+\widehat{CBD}=90^o\) (2)
\(\widehat{ACD}=\widehat{ACB}+\widehat{BCD}=90^o\) (3)
Từ (1) , (2) và (3) \(\Rightarrow\widehat{CBD=}\widehat{BCD}\)
Xét \(\Delta DBC\) có \(\widehat{CBD=}\widehat{BCD}\) (cmt)
\(\Rightarrow\Delta DBC\) cân tại \(D\) (đpcm)
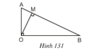
C1: Của lớp 9 nha
Xét tam giác ABO vuông tại O, đường cao OM có:
AB.OM = OA.OB ( Hệ thức lượng trong tam giác vuông )
C2: Của lớp 8 dùng đc nè
Xét \(\Delta\)ABO và \(\Delta\)OMA có:
Góc A : góc chung
góc AOB = góc AMO = 90 độ
=> \(\Delta\)ABO đồng dạng \(\Delta\)AMO (g.g)
=> \(\frac{AB}{OA}\)= \(\frac{OB}{OM}\)
=> AB.OM = OA.OB
Chúc bạn học tốt. C1 mình giới thiệu thêm nhé. Ngắn ngủn dễ dàng hơn C2 :)))