y*7/3+y:3/2=69
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KK
✎﹏Kim Kim✧❤‿✶🌈(*•.¸♡ţęąɱ ƒŗęę ƒįŗę...
3 tháng 8 2022
Đúng(2)
Những câu hỏi liên quan
NV
1
HH
4 tháng 2 2018
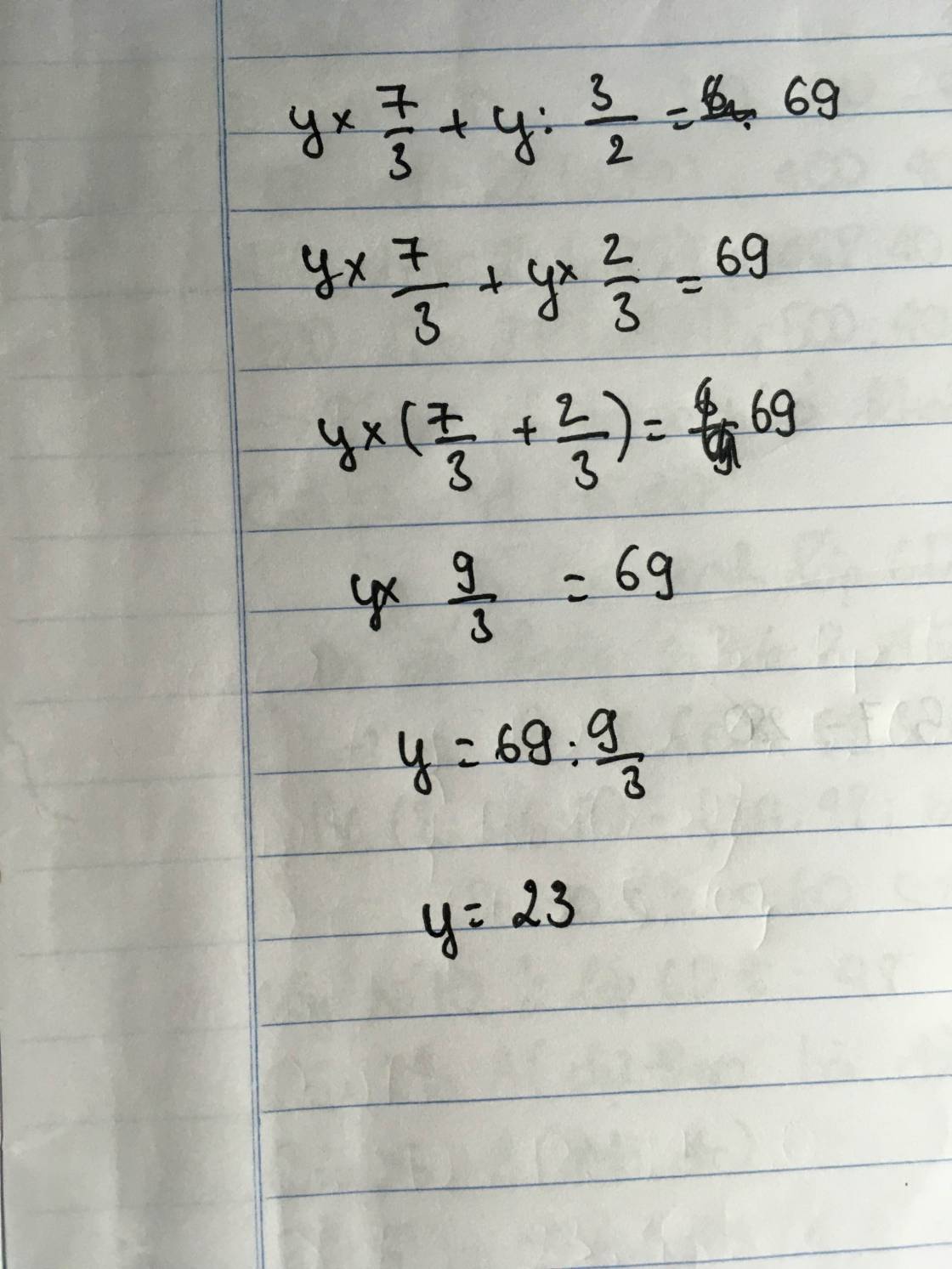
Giải:
a) \(-47+5y=3y-69\)
\(\Leftrightarrow5y-3y=-69+47\)
\(\Leftrightarrow2y=-22\)
\(\Leftrightarrow y=-\dfrac{22}{2}=-11\)
Vậy ...
b) \(\left(96-8y\right)+5y=-174\)
\(\Leftrightarrow96-8y+5y=-174\)
\(\Leftrightarrow96-3y=-174\)
\(\Leftrightarrow-3y=-174-96=-270\)
\(\Leftrightarrow y=\dfrac{-270}{-3}=90\)
Vậy ...
c) \(\left|7-2\right|=y+2\)
\(\Leftrightarrow5=y-2\)
\(\Leftrightarrow y=5+2=7\)
Vậy ...
25 tháng 3 2022
Bài 1. Tính rồi rút gọn:
a) 3/4 : 2/7 = 3/4 x 7/2 = 21/8
b) 3 : 3/5 = 3/1 x 5/3 = 15/3 = 5
c) 6/11 : 2/3 = 6/11 x 3/2 = 18/22 = 9/11
d) 15/4 : 5 = 15/4 x 1/5 = 15/20 = 3/4
Bài 2. Tìm y:
a) 6/7 x y = 5/14
y = 5/14 : 6/7
y = 5/14 x 7/6
y = 35/84
b) y : 2/3 = 4/9
y = 4/9 x 2/3
y = 8/27
LT
25 tháng 3 2022
1.
a.3/4 : 2/7 = 21/8
b. 3 : 3/5 = 5
c.6/11 : 2/3 = 9/11
d. 15/4 : 5 = 3/4
Tự ghi lại đề
HN
7 tháng 7 2017
1) Tìm x, y, z biết:
\(\dfrac{x}{5}=\dfrac{y}{6}\Rightarrow\dfrac{x}{20}=\dfrac{y}{24}\) (1)
\(\dfrac{y}{8}=\dfrac{z}{7}\Rightarrow\dfrac{y}{24}=\dfrac{z}{21}\) (2)
Từ (1) và (2) suy ra:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}\) và x + y - z = 69
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=\dfrac{x+y-z}{20+24-21}=\dfrac{69}{23}=3\)
\(\dfrac{x}{20}=3\Rightarrow\) x = 3 . 20 = 60
\(\dfrac{y}{24}=3\Rightarrow\) y = 3. 24 = 72
\(\dfrac{z}{21}=3\Rightarrow\) z = 3 . 21 = 63.
Q
7 tháng 12 2017
\(\frac{x}{2}=\frac{y}{3};\frac{y}{7}=\frac{z}{4}\Leftrightarrow\frac{x}{14}=\frac{y}{21}=\frac{z}{12}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{14}=\frac{y}{21}=\frac{z}{12}=\frac{x+y+z}{14+21+12}=\frac{69}{47}\)
\(\frac{x}{14}=\frac{69}{47}\Rightarrow x=\frac{966}{47}\)
\(\frac{y}{21}=\frac{69}{47}\Rightarrow y=\frac{1449}{47}\)
\(\frac{z}{12}=\frac{69}{47}\Rightarrow z=\frac{828}{47}\)
7 tháng 12 2017
Theo đề ra: \(\frac{x}{2}=\frac{y}{3}\)=> \(\frac{x}{14}=\frac{y}{21}\) (1)
\(\frac{y}{7}=\frac{z}{4}\)=> \(\frac{y}{21}=\frac{z}{12}\) (2)
Từ (1) và (2) => \(\frac{x}{14}=\frac{y}{21}=\frac{z}{12}\) và x + y + z = 69
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{14}=\frac{y}{21}=\frac{z}{12}=\frac{x+y+z}{14+21+12}=\frac{69}{47}\)
\(\frac{x}{14}=\frac{69}{47}=>x=\frac{69}{47}.14=\frac{966}{47}\)
\(\frac{y}{21}=\frac{69}{47}=>y=\frac{69}{47}.21=\frac{1449}{47}\)
\(\frac{z}{12}=\frac{69}{47}=>z=\frac{69}{47}.12=\frac{828}{47}\)
Vậy \(x=\frac{966}{47}\) , \(y=\frac{1449}{47}\), \(z=\frac{828}{47}\)
18 tháng 8 2016
\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{14}=\frac{y}{21}\)
\(\frac{y}{7}=\frac{z}{4}\Rightarrow\frac{y}{21}=\frac{z}{12}\)
\(\Leftrightarrow\frac{x}{14}=\frac{y}{21}=\frac{z}{12}=\frac{x+y-z}{14+21-12}=\frac{69}{23}=3\)
\(\Rightarrow x=52;y=63;z=36\)
18 tháng 8 2016
\(\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}\\\frac{y}{7}=\frac{z}{4}\end{cases}\Rightarrow\hept{\begin{cases}\frac{x}{14}=\frac{y}{21}\\\frac{y}{21}=\frac{z}{12}\end{cases}\Rightarrow}\frac{x}{14}=\frac{y}{21}=\frac{z}{12}}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{14}=\frac{y}{21}=\frac{z}{12}=\frac{x+y-z}{14+21-12}=\frac{69}{23}=3\)
\(\Rightarrow\hept{\begin{cases}x=3.14=42\\y=3.21=63\\z=3.12=36\end{cases}}\)
P
5 tháng 12 2021
Ta có:
x5=y6⇒x20=y24x5=y6⇒x20=y24 (1)(1)
y8=z7=y24=z21y8=z7=y24=z21 (2)(2)
Từ (1)(1) và (2)(2) ⇒x20=y24=z21⇒x20=y24=z21
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x20=y24=z21=x+y−z20+24−21=6923=3x20=y24=z21=x+y-z20+24-21=6923=3
⇒⎧⎪⎨⎪⎩x=60y=72z=63⇒{x=60y=72z=63
Vậy x=60;y=72x=60;y=72 và z=63
11 tháng 8 2016
1, ta co \(\frac{x}{5}=\frac{y}{6}=\frac{x}{20}=\frac{y}{24}\)
\(\frac{y}{8}=\frac{z}{7}=\frac{y}{24}=\frac{z}{21}\)
=>\(\frac{x}{20}=\frac{y}{24}=\frac{z}{21}=\frac{x+y-z}{20+24-21}=\frac{69}{23}=3\)
=>\(x=3\cdot20=60\)
\(y=3\cdot24=72\)
\(z=3\cdot21=63\)
11 tháng 8 2016
3. ta co \(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}=\frac{x+y-z+t}{15-7+3-1}=\frac{10}{10}=1\)
=> \(x=1\cdot15=15\)
\(y=1\cdot7=7\)
\(z=1\cdot3=3\)
\(t=1\cdot1=1\)