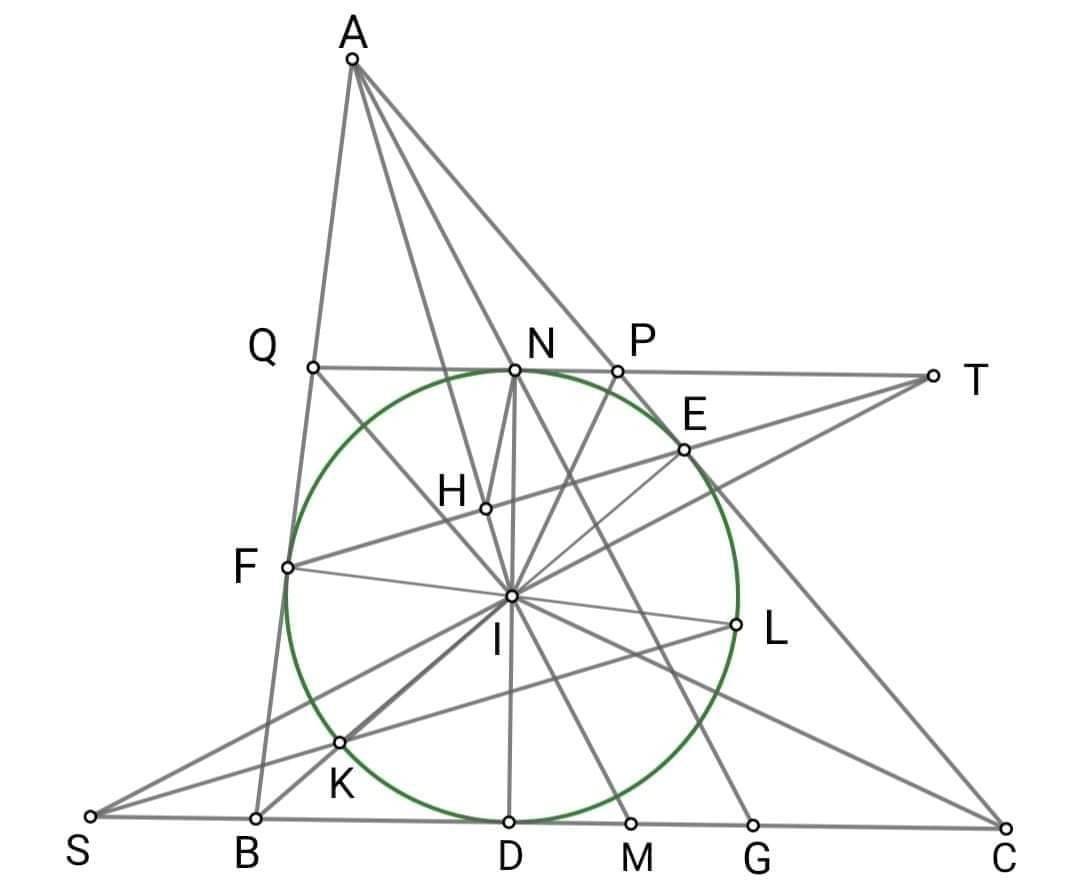
Cho đường tròn tâm \(I\) nội tiếp \(\Delta ABC\). Gọi các tiếp điểm của AB, BC, AC với I lần lượt là D, E, F. Một đường thẳng là tiếp tuyến tại P của I và song song với BC cắt AB, AC lần lượt tại M, N. Biết \(P_{ABC}=80,AC-AB=6.\)Tính AB, AC, BC để MN đạt giá trị lớn nhất.