cho tam giác ABC có AB <AC .
chứng minh góc ABC >góc ACB ( 2 cách )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DV
9
20 tháng 1 2018
cách thứ nhất AB=AC suy ra ABC cân tại A suy ra góc B=C
cách 2
có góc B đối diện với cạch AC
có góc C đối diện với cạnh AB
mà AC=AB suy ra B=C
ok 2 cách xin 1 cái tích
NN
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 1 2021
Cách 1: Từ A dựng đường cao AH (H thuộc BC)
Xét tg vuông ABH và tg vuông ACH có
AH chung
AB=AC
=> tg ABH = tg ACH (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng = nhau thì bằng nhau)
=> ^ABC = ^ACB
Cách 2: Dựng đường cao BD và CE (D thuộc AC và E thuộc AB)
\(S_{ABC}=\frac{AB.CE}{2}=\frac{AC.BD}{2}\Rightarrow CE=BD\)
Xét tg vuông BDC và tg vuông CEB có
BC chung
BD=CE (cmt)
=> tg BDC = tg CEB (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng = nhau thì bằng nhau)
=> ^ABC = ^ACB
NT
0
CG
28 tháng 7 2017
tuwj vex hinhf nha
1 a. xét tam giác abc có
góc a + góc b + góc c = 180 độ
t/s vào tính đc góc b + góc c= 120 độ
góc acb = 120 độ : ( 2+1).1=40 độ
b) xét tam giác abc có
góc a + góc b + góc c = 180 độ
t/s vào tính đc góc abc = 80 độ
có bi là tia phân giác của góc abc
=> góc abi = góc ibc = 80 độ :2=40 độ
có ci là tia phân giác của góc acb
=> góc aci = gócicb = 40 độ : 2 = 20 độ
xét tam giác ibc có
góc bic + góc ibc + bci = 180độ
thay số vào tính đc góc bic = 120 đọ( nghĩ z chứ chưa tính kĩ nha )
2
3 tháng 5 2023
Vì đường trung trực của `AC` cắt `AB` tại `D.`
`@` Theo tính chất của đường trung trực (điểm nằm trên đường trung trực của `1` đoạn thẳng thì cách `2` đầu mút đoạn thẳng đó)
`-> \text {DA = DC}`
Xét `\Delta ACD`: `\text {DA = DC}`
`-> \Delta ACD` cân tại `D.`
`-> \hat {A} = \hat {ACD}` `(1)`
Vì `\text {CD}` là tia phân giác của $\widehat {ACB} (g$$t)$
`->` $\widehat {ACD} = \widehat {BCD} =$ `1/2` $\widehat {ACB}$ `(2)`
Từ `(1)` và `(2)`
`->` $\widehat {ACB} = \widehat {2C_2} = \widehat {2A}$
Mà `\hat {A}=35^0`
`->` $\widehat {ACB}$`=35^0*2=70^0`
Xét `\Delta ABC`:
$\widehat {BAC} + \widehat {ABC}+ \widehat {ACB}=180^0 (\text {định lý tổng 3 góc trong 1 tam giác})$
`-> 35^0+` $\widehat {ABC} + 70^0=180^0$
`->` $\widehat {ABC}= 180^0-35^0-70^0=75^0$
Xét các đáp án trên `-> C (tm)`.
5 tháng 8 2023
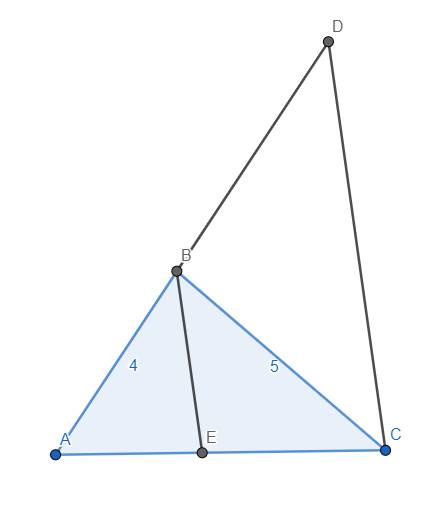
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.
b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)
Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\) nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\), suy ra \(AD=AB+BD=4+5=9\).
\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).
Vậy \(AC=6\)
5 tháng 8 2023
Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.
HT
4
10 tháng 12 2020
△ABC có AB= AC nê là tan giác cân.
➙góc ACB =góc ABC ( hai góc Đáy của một tam giác cân)
AM
10 tháng 12 2020
Kẻ đường trung tuyến AM, M thuộc BC
Xét hai tam giác ABM và ACM có:
\(\left\{{}\begin{matrix}AB=AC\\AMlacanhchung\\BM=MC\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta ABM=\Delta ACM\)\(\Rightarrow\)\(\widehat{ABC}=\widehat{ACB}\)
VT
0