Chứng minh rằng các tam giác ABC, A'B'C' có cùng trọng tâm khi và chỉ khi \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
16 tháng 4 2018
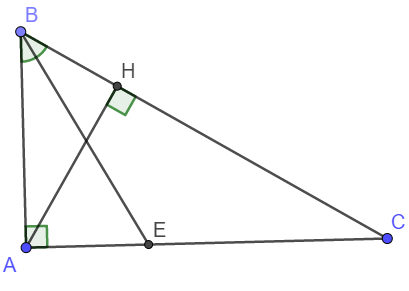
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
Góc B chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b)
Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
Góc C chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)
c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)
\(\Rightarrow HA=12\left(cm\right)\)
Khi đó áp dụng định lý Pi-ta-go ta có:
\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)
\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)
BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng tính chất tia phân giác trong tam giác ta có:
\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)
\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)
\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)
21 tháng 3 2023
1: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
2: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng vơi ΔABC
3: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF/HB=HE/HC
Xét ΔHFE và ΔHBC có
HF/HB=HE/HC
góc FHE=góc BHC
=>ΔFHE đồng dạng với ΔBHC
11 tháng 11 2015
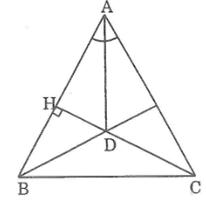
Tự ve hình nhé:
Góc CBK =DBK =60 => CBA=KBD mà BK=BC;BD=BA => Tam giác BKD =BCA (c-g-c)
=>DK =AC = AE.(1)
Tương tự Tam giác CKE =CBA => KE =AB =AD (2)
1;2 => AEKD là HBH ( có các cạnh đói = nhau)
b) DK =AC = CE
Hôm qua bận nên bạn thôn cảm nhé.
Gọi trọng tâm của tam giác ABC là G
Vì G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
+) Xét \(\overrightarrow{\text{AA}'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AG}+\overrightarrow{GA'}+\overrightarrow{BG}+\overrightarrow{GB'}+\overrightarrow{CG}+\overrightarrow{GC'}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)+\left(\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)-\overrightarrow{0}=\overrightarrow{0}\)
=> G đồng thời là trọng tâm của tam giác A'B'C'