60 59 60 61 P S R Q
Chứng minh đoạn thẳng PQ dài nhất trong hình trên (Trích từ cuộc thi Pink 2013)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 1 2021
a)Tính QR
Điểm Q nằm giữa 2 điểm R và P
QR+QP=PR
QR+4=6
QR=6-4=2
b)TÍNH PK và KQ
Điểm K là Trung điểm của đoạn PQ
KQ=KP=PQ:2=4:2=2
Điểm Q là TRUNG ĐIỂM CỦA ĐOẠN KR
vì :+Vì điểm Q nằm giũa 2 điểm K và R
+QK=QR=2CM
CM
15 tháng 9 2017
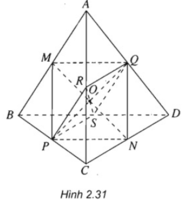
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
A
21 tháng 6 2019
a) Phân tích bài toán
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và\(\widehat{QPR}=60^0\). Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ∆PHQ = ∆PHR (cạnh huyền, cạnh góc vuông), suy ra \(\widehat{HPQ}=\widehat{HPR}=30^0\) Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ\(PH\perp d\) (H ∈ d). Dùng thước đo góc để vẽ góc HPx bằng 30°. Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ. Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR. Do HQ = HR nên PQ = PR.
Hơn nữa\(\widehat{QPR}=2\widehat{HQP}=60^0\)
b) Hướng dẫn
- Tam giác PQR có PQ = PR và \(\widehat{QPR}=60^0\), tam giác PQR là tam giác đều
PQ = 18cm => QR =18cm ; HQ = HR =9cm.
21 tháng 6 2019
Giả sử PQ và PR là hai đường xiên kẻ từ P đến d sao cho PQ = PR và ∠(QPR) = 60°.
Gọi H là chân đường vuông góc kẻ từ P đến d. Khi đó ΔPHQ = ΔPHQ (cạnh huyền, cạnh góc vuông),
suy ra ∠(HPQ) = ∠(HPR) = 30°. Từ đó suy ra cách vẽ hai đường xiên PQ và PR.
Kẻ PH ⊥ d (H ∈ d).
Dùng thước đo góc để vẽ góc HPx bằng 30°.
Tia Px cắt d tại điểm Q. Trên d lấy điểm R sao cho HR = HQ.
Hai đường xiên PQ và PR lần lượt có hình chiếu trên d là HQ và HR.
Do HQ = HR nên PQ = PR.
Hơn nữa ∠(QPR) = 2∠(HPQ) = 60°.
b) Hướng dẫn
- Tam giác PQR có PQ = PR và ∠(QPR) = 60°, tam giác đó là tam giác đều
- PQ = 18cm ⇒ QR =18 cm ; HQ = HR =9 cm
1 tháng 4 2022
a: Vì M là trung điểm của PQ
nên MQ=MP=3cm và QP=2MQ=6cm
b: Trên tia MQ, ta có: MQ<MK
nên điểm Q nằm giữa hai điểm M và K
mà MQ=1/2MK
nên Q là trung điểm của MK
TA
17 tháng 12 2017
a. độ dài đoạn thẳng QR là: QR=PR-PQ=6-4=2 cm
b. vì K là trung điểm của đoạn thẳng PQ nên độ dài đường thẳng KQ=4/2=2 (1)
Ta có:QR=2cm (theo câu a) (2)
Từ (1) và (2): KQ=QR=2cm
=> K là trung điểm đoạn thẳng KR
Xét \(\Delta PQR\)và \(\Delta SPR\)có
\(\hept{\begin{cases}\widehat{PQR}=\widehat{SPR}=59\\\widehat{PRQ}=\widehat{SRP}=61\\\widehat{RPQ}=\widehat{RSP}=60\end{cases}}\)
\(\Rightarrow\Delta PQR\)đồng dạng \(\Delta SPR\)
\(\frac{PQ}{SP}=\frac{PR}{SR}=\frac{QR}{PR}\)
Trong \(\Delta PQR\)và \(\Delta SPR\)cạnh PR trong \(\Delta SPR\)ứng với góc 60 còn trong tam giác còn lại ứng với góc 59 nên
\(\Delta PQR>\Delta SPR\)
=> cạnh lớn nhất trong \(\Delta PQR\)sẽ là đoạn thẳng dài nhất
Hay đoạn thẳng dài nhất là PQ (ứng với góc 61)
đoạn thẳng pr pải ko bn