Giải PT:
sinx + 4cosx =2 + 2sinx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MA
2
30 tháng 6 2021
a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)
b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)
Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)
\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)
Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)
Pttt:\(cos3x.cosa+sin3a.sina=1\)
\(\Leftrightarrow cos\left(3x-a\right)=1\)
\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))
Vậy...
LT
30 tháng 6 2021
1)\(1+2sinx=2cosx\)
\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)
\(\Leftrightarrow sin2x=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)
b) \(4cosx-3sinx=3\)
\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)
Khi đó:
\(sinacosx-cosasinx=\dfrac{3}{5}\)
\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
3)\(3cos3x+4sin3x=5\)
\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)
Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)
khi đó: \(sinacos3x+cosasin3x=1\)
\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)
Chúc bạn học tốt^^
17 tháng 8 2023
a: -1<=sin x<=1
=>-1+3<=sin x+3<=1+3
=>2<=sinx+3<=4
=>\(\dfrac{1}{2}>=\dfrac{1}{sinx+3}>=\dfrac{1}{4}\)
=>\(2>=\dfrac{4}{sinx+3}>=1\)
=>\(-2< =-\dfrac{4}{sinx+3}< =-1\)
=>-2+3<=y<=-1+3
=>1<=y<=2
y=1 khi \(\dfrac{-4}{sinx+3}+3=1\)
=>\(\dfrac{-4}{sinx+3}=-2\)
=>sinx+3=2
=>sin x=-1
=>x=-pi/2+k2pi
y=3 khi sin x=1
=>x=pi/2+k2pi
b: -1<=cosx<=1
=>4>=-4cosx>=-4
=>9>=-4cosx+5>=1
=>2/9<=2/5-4cosx<=2
=>2/9<=y<=2
\(y_{min}=\dfrac{2}{9}\) khi \(\dfrac{2}{5-4cosx}=\dfrac{2}{9}\)
=>\(5-4\cdot cosx=9\)
=>4*cosx=4
=>cosx=1
=>x=k2pi
y max khi cosx=-1
=>x=pi+k2pi
c: \(0< =cos^2x< =1\)
=>\(0< =2\cdot cos^2x< =2\)
=>\(-1< =y< =2\)
y min=-1 khi cos^2x=0
=>x=pi/2+kpi
y max=2 khi cos^2x=1
=>sin^2x=0
=>x=kpi
31 tháng 7 2023
a: tan x=căn 3
=>sin x/cosx=căn 3
=>sin x=cosx*căn 3
\(A=\dfrac{\left(cosx\cdot\sqrt{3}\right)^2}{\left(cosx\cdot\sqrt{3}\right)^2-cos^2x}=\dfrac{3}{3-1}=\dfrac{3}{2}\)
b: cot x=-căn 3
=>cosx=-sinx*căn 3
\(A=\dfrac{sinx+4\cdot sinx\cdot\sqrt{3}}{2\cdot sinx+sinx\cdot\sqrt{3}}=\dfrac{1+4\sqrt{3}}{2+\sqrt{3}}=\left(4\sqrt{3}+1\right)\left(2-\sqrt{3}\right)\)
=8căn 3-12+2-căn 3
=7căn 3-10
AH
Akai Haruma
Giáo viên
31 tháng 7 2023
Lời giải:
\(A=\frac{1}{\frac{\sin ^2x-\cos ^2x}{\sin ^2x}}=\frac{1}{1-(\frac{\cos x}{\sin x})^2}=\frac{1}{1-(\frac{1}{\tan x})^2}=\frac{1}{1-(\frac{1}{\sqrt{3}})^2}=\frac{3}{2}\)
\(A=\frac{\sin x-4\cos x}{2\sin x-\cos x}=\frac{1-4.\frac{\cos x}{\sin x}}{2-\frac{\cos x}{\sin x}}=\frac{1-4\cot x}{2-\cot x}=\frac{1-4.(-\sqrt{3})}{2-(-\sqrt{3})}=-10+7\sqrt{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 5 2020
\(A=\frac{3sinx-4cosx}{cosx+2sinx}=\frac{\frac{3sinx}{cosx}-4}{1+\frac{2sinx}{cosx}}=\frac{3tanx-4}{1+2tanx}=\frac{3.5-4}{1+2.5}=...\)
\(B=\frac{\frac{sinx}{cos^3x}+\frac{sin^3x}{cos^3x}}{\frac{3cos^3x}{cos^3x}+\frac{cosx}{cos^3x}}=\frac{tanx.\frac{1}{cos^2x}+tan^3x}{3+\frac{1}{cos^2x}}=\frac{tanx\left(1+tan^2x\right)+tan^3x}{3+\left(1+tan^2x\right)}=\frac{5\left(1+5^2\right)+5^3}{3+1+5^2}=...\)
PT
1
KN
1
YN
17 tháng 12 2021
Answer:
\(\sin x+4\cos x=2+\sin2x\)
\(\Leftrightarrow\sin x-2+4\cos x-2\sin x\cos x=0\)
\(\Leftrightarrow\sin x-2+2\cos x\left(2-\sin x\right)=0\)
\(\Leftrightarrow\left(\sin x-2\right)\left(1-2\cos x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sin x=2\text{(Loại)}\\\cos x=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow x=\pm\frac{\text{π}}{3}+k2\text{π}\left(k\inℤ\right)\)
CM
3 tháng 11 2018
3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
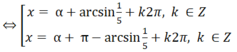
`sin x+4 cos x=2+2sin x`
`<=>sin x-4 cos x=-2`
`<=>\sqrt{17}(1/\sqrt{17} sin x-4/\sqrt{17} cos x)=-2`
`<=>1/\sqrt{17} sin x-4/\sqrt{17} cos x=-2/\sqrt{17}`
Đặt `cos \alpha=1/\sqrt{17}` ; `sin \alpha= 4/\sqrt{17}`
`=>cos \alpha sin x-sin \alpha cos x=-2/\sqrt{17}`
`<=>sin(x-\alpha)=-2/\sqrt{17}`
`<=>` $\left[\begin{matrix} x-\alpha=arc sin (\dfrac{-2}{\sqrt{17}})+k2\pi\\ x-\alpha=\pi-arc sin (\dfrac{-2}{\sqrt{17}})+k2\pi\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x=\alpha+arc sin (\dfrac{-2}{\sqrt{17}})+k2\pi\\ x=\alpha+\pi-arc sin (\dfrac{-2}{\sqrt{17}})+k2\pi\end{matrix}\right.$ `(k in ZZ)`
Vậy `S={\alpha+arc sin ([-2]/\sqrt{17})+k2\pi,\alpha+\pi-arc sin ([-2]/\sqrt{17})+k2\pi|k in ZZ,cos \alpha=1/\sqrt{17}` ; `sin \alpha= 4/\sqrt{17}}`
ngưỡng mộ cj gkee:33