Question

[Ta Ro]

Thầy cô ơi giúp e giải bài này với ạ. Em cảm ơn Bài 7 : Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi M là một điểm chuyển động trên nửa đường tròn đó. Tiếp tuyến tại M của (O) cắt các tiếp tuyến Ax tại A và tiếp tuyến By tại B của (O) ở C và D. a/ Chứng minh: OACM và OBDM nội tiếp. b/ Chứng minh: ACO  MBD c/ Nối OC và OD cắt AM và BM tại E và F. Tìm quỹ tích trung điểm I của EF ?

Answer 1

[νì ¢υộ¢ đờι ℓà инữиɢ иιềм đαυ]

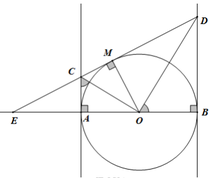
Bạn tự vẽ hình nha!

c) Các tam giác ACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90^o.

Mặt khác g.AMB =90^o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)

Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.