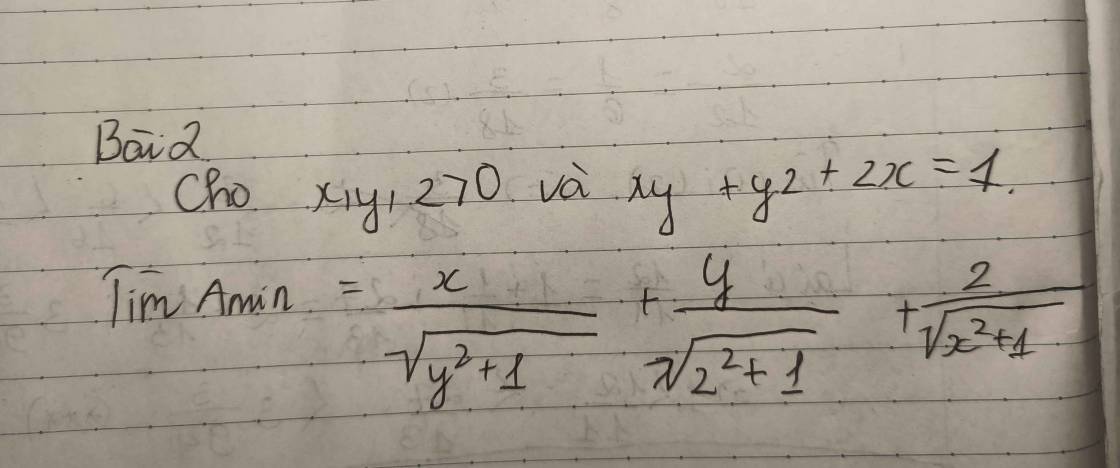Tìm A min.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2023
a.
\(F=\dfrac{a}{b+2}\Rightarrow F.b+2F=a\)
\(\Rightarrow2F=a-F.b\)
\(\Rightarrow4F^2=\left(a-F.b\right)^2\le\left(a^2+b^2\right)\left(1^2+F^2\right)=F^2+1\)
\(\Rightarrow3F^2\le1\)
\(\Rightarrow-\dfrac{1}{\sqrt{3}}\le F\le\dfrac{1}{\sqrt{3}}\)
Dấu "=" lần lượt xảy ra tại \(\left(a;b\right)=\left(-\dfrac{\sqrt{3}}{2};-\dfrac{1}{2}\right)\) và \(\left(\dfrac{\sqrt{3}}{2};-\dfrac{1}{2}\right)\)
b. Đặt \(\left\{{}\begin{matrix}a+b=x\\a-2b=y\end{matrix}\right.\) quay về câu a
ML
8 tháng 8 2015
Một số bất đẳng thức thường được dùng (chứng minh rất đơn giản)
Với a, b > 0, ta có:
\(a^2+b^2\ge2ab\)
\(\left(a+b\right)^2\ge4ab\)
\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)
Dấu "=" của các bất đẳng thức trên đều xảy ra khi a = b.
Phân phối số hạng hợp lí để áp dụng Côsi
\(1\text{) }P=\frac{1}{a^2+b^2}+\frac{1}{2ab}+\frac{1}{2ab}\ge\frac{4}{a^2+b^2+2ab}+\frac{1}{\frac{\left(a+b\right)^2}{2}}=\frac{4}{\left(a+b\right)^2}+\frac{2}{\left(a+b\right)^2}\)
\(\ge6\)
Dấu "=" xảy ra khi a = b = 1/2.
\(2\text{) }P\ge\frac{4}{a^2+b^2+2ab}=\frac{4}{\left(a+b\right)^2}\ge4\)
\(3\text{) }P=\frac{1}{a^2+b^2}+\frac{1}{2ab}+\frac{1}{4ab}+4ab+\frac{1}{4ab}\)
\(\ge\frac{1}{\left(a+b\right)^2}+2\sqrt{\frac{1}{4ab}.4ab}+\frac{1}{\left(a+b\right)^2}\ge1+2+1=4\)
10 tháng 11 2021
\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
17 tháng 3 2021
Lời giải:
Áp dụng BĐT AM-GM:
$P=(a+1)+\frac{2}{a+1}+2\geq 2\sqrt{(a+1).\frac{2}{a+1}}+2=2\sqrt{2}+2$
Vậy $P_{\min}=2\sqrt{2}+2$
Giá trị này đạt tại $(a+1)^2=2; a>0\Leftrightarrow a=\sqrt{2}-1$
------------------------
Bổ sung ĐK: $a>1$
$X=\frac{a^2-1+2}{a-1}=a+1+\frac{2}{a-1}$
$=(a-1)+\frac{2}{a-1}+2$
$\geq 2\sqrt{2}+2$ (AM-GM)
Vậy $X_{\min}=2\sqrt{2}+2$
Giá trị đạt tại $(a-1)^2=\sqrt{2}; a>1\Leftrightarrow a=\sqrt{2}+1$
\(A=\dfrac{x}{\sqrt{y^2+1}}+\dfrac{y}{\sqrt{z^2+1}}+\dfrac{z}{\sqrt{x^2+1}}\)
\(=\dfrac{x}{\sqrt{y^2+xy+yz+zx}}+\dfrac{y}{\sqrt{z^2+xy+yz+zx}}+\dfrac{z}{\sqrt{x^2+xy+yz+zx}}\)
\(=\dfrac{x}{\sqrt{y\left(y+x\right)+z\left(y+x\right)}}+\dfrac{y}{\sqrt{z\left(z+x\right)+y\left(z+x\right)}}+\dfrac{z}{\sqrt{x\left(x+y\right)+z\left(x+y\right)}}\)
\(=\dfrac{x}{\sqrt{\left(y+x\right)\left(y+z\right)}}+\dfrac{y}{\sqrt{\left(z+x\right)\left(z+y\right)}}+\dfrac{z}{\sqrt{\left(x+y\right)\left(x+z\right)}}\)
\(\ge^{Caushy}\dfrac{x}{\dfrac{\left(y+x\right)+\left(y+z\right)}{2}}+\dfrac{y}{\dfrac{\left(z+x\right)+\left(z+y\right)}{2}}+\dfrac{z}{\dfrac{\left(x+y\right)+\left(x+z\right)}{2}}\)
\(=\dfrac{2x}{2y+x+z}+\dfrac{2y}{2z+x+y}+\dfrac{2z}{2x+y+z}\)
\(=2\left(\dfrac{x^2}{2yx+x^2+zx}+\dfrac{y^2}{2zy+xy+y^2}+\dfrac{z^2}{2xz+yz+z^2}\right)\)
\(\ge^{Caushy-Schwarz}2.\dfrac{\left(x+y+z\right)^2}{2yx+x^2+zx+2zy+xy+y^2+2xz+yz+z^2}\)
\(=2.\dfrac{\left(x+y+z\right)^2}{\left(x^2+y^2+z^2+2xy+2yz+2zx\right)+\left(xy+yz+zx\right)}\)
\(=2.\dfrac{\left(x+y+z\right)^2}{\left(x+y+z\right)^2+1}\)
Đặt \(\left(x+y+z\right)^2=t^2\). Ta có:
\(A\ge\dfrac{2t^2}{t^2+1}=\dfrac{2t^2+2-2}{t^2+1}=2-\dfrac{2}{t^2+1}\).
Ta lại có: \(t^2=\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)=3.1=3\)
\(\Rightarrow A\ge2-\dfrac{2}{3+1}=\dfrac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\dfrac{\sqrt{3}}{3}\)
Vậy \(MinA=\dfrac{3}{2}\)