Đạo hàm giúp e vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KB
7 tháng 5 2022
a.\(y'=x\left(\sqrt{x^2-2x}\right)'+\sqrt{x^2-2x}=\dfrac{x}{2\sqrt{x^2-2x}}2\left(x-1\right)+\sqrt{x^2-2x}=\dfrac{x\left(x-1\right)}{\sqrt{x^2-2x}}+\sqrt{x^2-2x}\)
\(=\dfrac{x^2-x+x^2-2x}{2\sqrt{x^2-2x}}=\dfrac{2x^2-3x}{2\sqrt{x^2-2x}}\)
b. \(y=3sin2x+cos3x\Rightarrow y'=6cos2x-3sin3x\)
KB
3 tháng 5 2022
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
c.
\(y'=\dfrac{\left(2x-1\right)'\left(4x-3\right)-\left(4x-3\right)'\left(2x-1\right)}{\left(4x-3\right)^2}=\dfrac{2\left(4x-3\right)-4\left(2x-1\right)}{\left(4x-3\right)^2}\)
\(=\dfrac{-2}{\left(4x-3\right)^2}\)
d.
\(y'=-\dfrac{3.\left(2x+1\right)'}{\left(2x+1\right)^2}=-\dfrac{6}{\left(2x+1\right)^2}\)
PT
1
CM
13 tháng 10 2017
Nhận thấy có dạng 
Áp dụng, ta được 
Tính ln[ln(x)]'
Nhận thấy có dạng 
Áp dụng, ta được
NB
1
PT
1
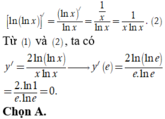
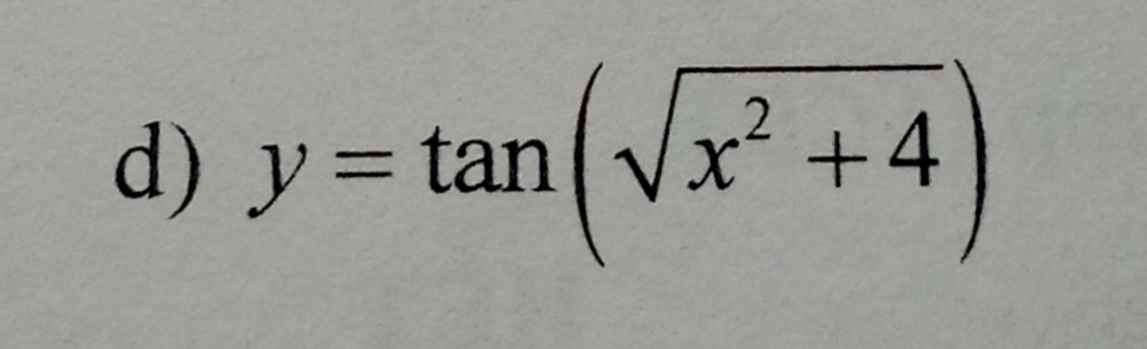
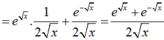
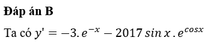
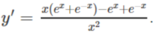
Anh chị tham khảo thử ạ:
Ta có: \(f\left(x\right)=\dfrac{2\sqrt{x}+m}{\sqrt{x+1}}\left(x\ge0\right)\)
\(\Rightarrow\)\(f'\left(x\right)=\dfrac{2.\dfrac{\sqrt{x+1}}{2\sqrt{x}}-\left(\sqrt{x}+m\right).\dfrac{1}{2\sqrt{x+1}}}{x+1}\)
\(\Rightarrow f'\left(x\right)=\dfrac{\dfrac{\sqrt{x+1}}{\sqrt{x}}-\dfrac{\sqrt{x}+m}{2\sqrt{x+1}}}{x+1}\)