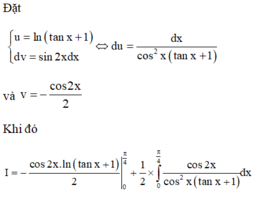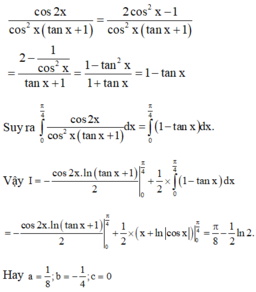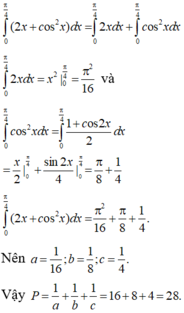BÀI 1
a) tìm a,b,c biết rằng ab+c ;bc+4a; ac=9b
b)tìm \(x,y\in Z\)biết \(\frac{x}{8}-\frac{1}{y}=\frac{1}{4}\Rightarrow\frac{1}{y}=\frac{x}{8}-\frac{1}{4}\)
c) tìm giá trị nhỏ nhất của biểu thức
BÀI 2 Hai xe cùng khởi hành một lúc từ A và B. Xe thứ nhất đến B hết 8h xe thứ hai đến A hết 6h. khi hai xe gặp nhau thì xe thứ nhất hơn xe thứ hai là 20 km. Tính quãng đường AB
( làm theo dạng tìm x đại lượng tỉ lệ thuận -đại lượng tỉ lệ nghịch )
BÀI3 cho tam giác ABC ,M là trung điểm của BC. trên tia đối của của MA lấy ME sao cho ME=MA
a) chứng minh AC // BE
b) gọi I là 1 điểm bất kì trênAC,K là 1 điểm bất kì trên BE sao cho AI =EK. Chứng minh ba điểm I,M,K thẳng hàng