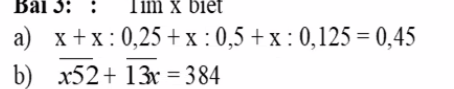Giúp mình với ạ.Mình đang cần gấp ạ
Giúp mình với ạ.Mình đang cần gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a) ( x - 4 ) . 3 = 21
x - 4 = 21 : 3
x - 4 = 7
x = 7 + 4
x = 11
b) 585 - ( 7x + 60 ) = 455
7x + 60 = 585 - 455
7x + 60 = 130
7x = 130 - 60
7x = 70
x = 70 : 7
x = 10
44 + ( 16 - x ) = 50
=> 16 - x = 50 - 44
=>16 - x = 6
=> x = 16 - 6
=> x = 10

Lời giải:
Cộng 3 PT lại ta có:
$x(a+b+c)+y(a+b+c)=a+b+c$
$\Leftrightarrow (a+b+c)(x+y-1)=0$
$\Rightarrow a+b+c=0$ hoặc $x+y-1=0$
TH1: $a+b+c=0\Leftrightarrow a+b=-c$
Khi đó: $a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=3abc$
$\Rightarrow \frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=3$ (đpcm)
TH2: $x+y-1=0\Leftrightarrow y=1-x$
Thay vô hpt \(\left\{\begin{matrix} ax+b(1-x)=c\\ bx+c(1-x)=a\\ cx+a(1-x)=b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x(a-b)=c-b\\ x(b-c)=a-c\\ x(c-a)=b-a\end{matrix}\right.\)
\(\Rightarrow x^3(a-b)(b-c)(c-a)=(c-b)(a-c)(b-a)=-(a-b)(b-c)(c-a)\)
\(\Leftrightarrow (a-b)(b-c)(c-a)(x^3+1)=0\)
Nếu $a-b=0$ thì kéo theo $b-c=c-a=0$
$\Rightarrow a=b=c$
Nếu $b-c=0; c-a=0$ thì tương tự
Nếu $x^3+1=0\Leftrightarrow x=-1$
$\Rightarrow b-a=c-b=a-c\Rightarrow a=b=c$
Tóm lại $a=b=c$
Do đó: $\frac{a^2}{bc}+\frac{b^2}{ac}+\frac{c^2}{ab}=1+1+1=3$ (đpcm)

- Đầu tiên bạn cần xác định được alen trội và lặn. Ví dụ như ta quy ước $A$ là quả to là trội, còn $a$ là quả bé lặn.
- Tiếp theo là ở $P$ thì nếu bài nói quả to thuần chủng thì tức kiểu gen ở đây là $AA$ còn nếu không thuần chủng thì là $Aa$ còn nếu nói quả to không thì có 2 trường hợp.
- Ví dụ như ở phép lai giữa quả to thuần chủng với quả nhỏ.
$P:$ $AA$ \(\times\) \(aa\)
$Gp:$ $A$ $a$
$F_1:$ $Aa$
- Ở $Gp$ thì bạn cần phải rõ là $AA$ sẽ tạo ra $A$ còn $Aa$ sẽ tạo ra 2 giao tử $A,a$ và kết hợp với giao tử bên còn lại tạo $F1$
- Ở phép lai 1 cặp tính trạng có 6 trường hợp:
\(1.\) \(P:AA\times AA\rightarrow F_1:100\%AA\)
\(2.\) \(P:AA\times Aa\rightarrow F_1:50\%AA;50\%Aa\)
\(3.\) \(P:AA\times aa\rightarrow F_1:100\%Aa\)
\(4.\) \(P:Aa\times Aa\rightarrow F_1:25\%AA;50\%Aa;25\%aa\)
\(5.\) \(P:Aa\times aa\rightarrow F_1:50\%Aa;50\%aa\)
\(6.\) \(P:aa\times aa\rightarrow F_1:100\%aa\)

bn ơi đề bài là 934 hay 936 học sinh ạ? tại mk chia thấy ns dư