kẻ tia phân giác ax, by của 1 cặp góc so le trong tạo bởi đường thẳng b vuông góc vs 2 đường thẳng song songc và d. Chứng minh rằng ax và by nàm trong 2 đường thẳng song song
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2023
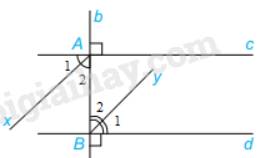
Vì Ax là tia phân giác của góc A vuông nên \(\widehat {{A_1}} = \widehat {{A_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì By là tia phân giác của góc B vuông nên \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_2}}( = 45^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết hai đường thẳng song song)
TM
1 tháng 11 2017
Hướng dẫn cách làm (nhớ vẽ hình và ghi GT, KL nha):
Từ a//b suy ra 2 góc so le trong bất kì(1) bằng nhau, rồi từ Ax và By là 2 tia phân giác của 2 góc đó rồi suy ra Ax // By vì có cặp góc so le trong tạo bởi 2 góc là nửa của 2 góc so le trong bất kì đó(1)
7 tháng 12 2023
a: Xét ΔMHA vuông tại H và ΔMKB vuông tại K có
MA=MB
\(\widehat{MAH}=\widehat{MBK}\)(hai góc so le trong, AH//BK)
Do đó: ΔMHA=ΔMKB
=>MH=MK
b: Ta có: ΔMHA=ΔMKB
=>\(\widehat{HMA}=\widehat{KMB}\)
mà \(\widehat{KMB}+\widehat{KMA}=180^0\)(hai góc kề bù)
nên \(\widehat{HMA}+\widehat{KMA}=180^0\)
=>\(\widehat{HMK}=180^0\)
=>H,M,K thẳng hàng