Hỏi trọng tâm của tam giác đều có cách đều 3 cạch của nó hay không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


GT tam giác ABC đều
G là trọng tâm tam giác
KL G cách đề ba cạnh tam giác
Trọng tâm của tam giác đều cách đều ba cạnh của nó :
Giả sử ∆ABC đều có trọng tâm G
=> GA = 2323AN; GB = 2323BM; GC = 2323EC
Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau
=> GA = GB = GC
Do đó: ∆AMG = ∆CMG (c.c.c)
=> ˆAMG=ˆCMGAMG^=CMG^
Mà ˆAMG=ˆCMGAMG^=CMG^ = 1800
=> ˆAMGAMG^ = 900
=> GM ⊥ AC tức là GM khoảng cách từ G đến AC
Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, AC
Mà GM =1313BM; GN = 1313AN; EG = 1313EC
Và AN = BM = EC nên GM = GN = GE
Hay G cách đều ba cạnh của tam giác ABC

Trọng tâm của tam giác đều cách đều ba cạnh của nó :
Giả sử ∆ABC đều có trọng tâm G
=> GA = AN; GB = BM; GC = EC
Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau
=> GA = GB = GC
Do đó: ∆AMG = ∆CMG (c.c.c)
=>
Mà = 1800
=> = 900
=> GM ⊥ AC tức là GM khoảng cách từ G đến AC
Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, AC
Mà GM =BM; GN = AN; EG = EC
Và AN = BM = EC nên GM = GN = GE
Hay G cách đều ba cạnh của tam giác ABC

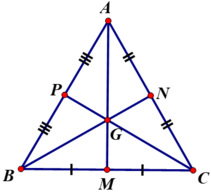
- Gọi G là trọng tâm ΔABC đều
AM, BN, CP là các đường trung tuyến của ΔABC
Theo tính chất trọng tâm tam giác :
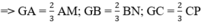
Vì ΔABC đều nên ba trung tuyến AM = BN = CP (áp dụng chứng minh bài 29)
Suy ra: GA = GB = GC
Và AM – GA = BN – GB = CP – GC hay GM = GN = GP
- ΔANG và ΔCNG
GN chung
GA = GC (chứng minh trên)
NA = NC ( N là trung điểm AC)
⇒ ΔANG = ΔCNG (c.c.c)
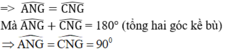
⇒ GN ⊥ AC tức là GN là khoảng cách từ G đến AC.
Chứng minh tương tự GM, GP là khoảng cách từ G đến BC, AB.
- Mà GM = GN = GP (chứng minh trên)
Vậy G cách đều ba cạnh của tam giác ABC.


Trọng tâm của tam giác đều cách đều ba cạnh của nó :
Giả sử ∆ABC đều có trọng tâm G
=> GA = AN; GB =
BM; GC =
EC
Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau
=> GA = GB = GC
Do đó: ∆AMG = ∆CMG (c.c.c)
=>
Mà = 1800
=> = 900
=> GM ⊥ AC tức là GM khoảng cách từ G đến AC
Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, AC
Mà GM =BM; GN =
AN; EG =
EC
Và AN = BM = EC nên GM = GN = GE
Hay G cách đều ba cạnh của tam giác ABC
Trọng tâm của một tam giác đều có cách đều ba cạnh của nó
Vì đơn giản, trong tam giác đều, trọng tâm cũng là trực tâm

trong tam cua tg deu chinh la tam dg tron ngoai tiep va noi tiep nen no cach deu 3 canh vi trong tg deu
dg cao, dg trung tuyen ,dg pg , tt trung nhau


giao điểm của 3 đường phân giác trong của một tam giác
A,cách đều 3 cạnh của tam giác đó
B,là điểm luôn thuộc một cạch của tam giác đó
C,cách đều 3 đỉnh của tam giác đó
D,là trọng tâm của tam giác đó
Theo mình là có vì trong tam giác đều 3 đường trung tuyến cũng chính là 3 đường phân giác của tam giác vậy điểm trọng tâm là giao điểm của 3 đường trung tuyến thì cũng là giao điểm của 3 tia đường phân giác của tam giác. mà giao điểm của 3 đường phân giác của cùng 1tam giác thì cách đều 3 cạnh suy ra trọng tâm của 1 tam giác cách đều 3 cạnh của tam giác
Trọng tâm của một tam giác đều có cách đều ba cạnh của nó
Vì đơn giản, trong tam giác đều, trọng tâm cũng là trực tâm