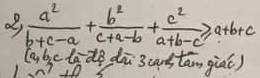
các bạn giúp mình chứng minh cái này với. khó quá mình nghĩ mãi chả ra
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:25.12511 < 12811.25 < 277.32 = 282
=> 25.12511 < 282
=> 535 < 282
=> 1035 < 2117
Ta có:
2^96 = 4096^8
2^96 < 41^8.10^16
2^81 < 2.41^8.5^16...(*)
Lại có: 9.2^13 < 9.8200 < 73000 < 625.125
=> 9.2^13 < 5^7
=> 300^2.2^9 < 5^11
=> 17^4.2^9 < 5^11...(vì 17^2 <300)
=> 1700^4.2 < 5^19
=> 2.41^8 < 5^19 ...(vì 41^2 <1700)
=> 2.41^8.5^16 < 5^35
kết hợp với (*) => 2^81 < 5^35
Suy ra:đpcm
=> 2^81 < 5^35 < 2^81
=> 2^116 < 10^35 < 2^117....đpcm
\(10^{35}=2^{35}.5^{35}\)
\(2^{116}=2^{35}.2^{81};2^{117}=2^{35}.2^{82}\)
can C/m
\(2^{81}<5^{35}<2^{82}\)
C/M
\(5^{35}<2^{82}\)(nang mu len 7.3=21 )
\(5^{35.21}<2^{82.21}\Leftrightarrow\left(5^3\right)^{^{7.35}}<\left(2^7\right)^{^{3.82}}\Leftrightarrow125^{245}<128^{246}\)=.> dpcm
50% xem the nao da

Bn tự vẽ hình nha
Xét tg AHB và tg AHC có
AB=AC; góc AHB = góc AHC =90 độ;
Ah cạnh chung
=> tg AHB = tg AHC (ch cgv)
=> BH = HC
=> H là trung điểm BC
Xét tg BKC có
H là trung điểm BC (cmt)
DH//KC ( gt)
=> D là trung điểm BK
( đpcm )
Ầy mk chỉ biết câu a thui mà đằng nào chúng ta mới 2k5 thui biết vận dụng cả lớp 8 là tốt lắm rùi ....!

gọi Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.

dễ dàng nhận thấy AP // CM vì góc DAP = góc BCM. Tương tự ta có EF//HG
vậy tứ giác EFGH là hình bình hành
Vì ABCD là hình bình hành nên
góc B+C = 180
xét tam giác CGB
có góc B+C = 180 : 2 = 90 vậy góc G = 90
xét hình bình hành EFGH có 1 góc vuông nên đó là hình chữ nhật

theo em thì chị hoặc anh chỉ cần lấy số phút chia số góc thôi ạ
12 giờ x 60 phút chia tất cả cho 360o
sẽ ra 1 phút tương ứng vói bao nhiêu độ
từ đó mà 7h50p cũng vậy

\(\left(\Sigma\frac{1}{\left(a+b\right)^2}\right)\left(2abc+\Sigma a^2\left(b+c\right)\right)=\Sigma\frac{a\left(b+c\right)^2+\left(a^2+bc\right)\left(b+c\right)}{\left(b+c\right)^2}=\Sigma a+\Sigma\frac{a^2+bc}{b+c}\)
Mặt khác ta có :
\(\left(\Sigma\frac{a^2+bc}{b+c}\right)\left(\Sigma a\right)=\Sigma\frac{a^3+abc}{b+c}+\Sigma\left(a^2+bc\right)\) ( nhân vào xong tách )
\(=\Sigma\frac{a^3+abc}{b+c}-\Sigma a^2+\Sigma\left(2a^2+bc\right)=\Sigma\frac{a\left(a-b\right)\left(a-c\right)}{b+c}+\Sigma\left(2a^2+bc\right)\) ( * )
Theo BĐT Vornicu Schur chứng minh được ( * ) không âm.
do đó : \(\Sigma\frac{a^2+bc}{b+c}\ge\frac{\Sigma\left(2a^2+bc\right)}{\Sigma a}\)
Theo đề bài , cần chứng minh : \(\left(\Sigma ab\right)\left(\Sigma\frac{1}{\left(a+b\right)^2}\right)\ge\frac{9}{4}\)
Kết hợp với dòng đầu tiên t cần c/m :
\(\left(\Sigma ab\right)\left(\Sigma a+\frac{\Sigma\left(2a^2+bc\right)}{\Sigma a}\right)\ge\frac{9}{4}\left(2abc+\Sigma a^2\left(b+c\right)\right)\)
Quy đồng lên, ta được :
\(\Sigma a^3\left(b+c\right)\ge2\Sigma\left(ab\right)^2\Leftrightarrow\Sigma ab\left(a-b\right)^2\ge0\)
\(\Rightarrow\)đpcm

\(A=\dfrac{2x+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{4\sqrt{x}}\ge2\sqrt{\dfrac{\sqrt{x}}{8\sqrt{x}}}=2\sqrt{\dfrac{1}{8}}=\dfrac{\sqrt{2}}{2}=\dfrac{1}{2}\cdot\sqrt{2}>\dfrac{1}{2}\left(cosi\right)\)
Áp dụng BĐT \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}\)(a,b,c,x,y,z > 0)
Vì a,b,c là độ dài 3 cạnh của tam giác nên a,b,c > 0
Áp dụng BĐT tam giác, ta có a < b + c, b < c + a, c < a + b
=> b + c - a, c + a - b, a + b - c > 0
Khi đó, ta có \(\dfrac{a^2}{b+c-a}+\dfrac{b^2}{c+a-b}+\dfrac{c^2}{a+b-c}\ge\dfrac{\left(a+b+c\right)^2}{a+b+c}=a+b+c\)
(đpcm).Dấu = xảy ra <=> a = b = c