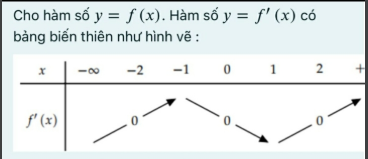
từ bảng biến thiên trên hãy lập bảng xét dấu của f'(x)
Giúp em với ạ em cảm ơn nhìu!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2023
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |
b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
13 tháng 2 2023
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |
b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
CM
6 tháng 4 2019
Chọn B
Đặt 
Bài toán quy về tìm giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0].
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0] là 3.
Vậy giá trị lớn nhất của hàm số f(sin x -1) bằng 3.
CM
13 tháng 6 2018
1.TXĐ: D = R.
3. Bảng biến thiên:
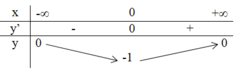
Vậy giá trị nhỏ nhất của hàm số đã cho là – 1 tại x = 0.
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
\(y'=-2cos2x=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}\\x=\dfrac{\pi}{4}\end{matrix}\right.\)
BBT:
Hàm đồng biến trên \(\left(-\dfrac{\pi}{4};\dfrac{\pi}{4}\right)\) và nghịch biến trên các khoảng \(\left(-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right);\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\)
14 tháng 10 2021
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
TB
14 tháng 10 2021
Cái này là xét sự biến thiên: nghịch biến hay đồng biến chứ ạ???
DD
Đoàn Đức Hà
Giáo viên
25 tháng 5 2022
Bài 6:
a) Dấu hiệu cần tìm hiểu ở đây là số con của mỗi gia đình trong \(30\) gia đình thuộc một thôn.
Bảng tần số:
| Số con | 0 | 1 | 2 | 3 | 4 | |
| Tần số | 2 | 4 | 17 | 5 | 2 | N=30 |
b) Nhận xét:
- Số con của các gia đình thuộc khoảng từ 0 đến 4 con.
- Số con trong các gia đình trong thôn chủ yếu là 2 con, chiếm khoảng 56,67%.
28 tháng 12 2020
a, (1) có nghiệm duy nhất trên [-2 ; 2] khi
[-2 ; 2] khi \(\left[{}\begin{matrix}-4m=-8\\1\ge-4m>-7\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}m=2\\\dfrac{-1}{4}\le m< \dfrac{7}{4}\end{matrix}\right.\) hay m ϵ [\(\dfrac{-1}{4};\dfrac{7}{4}\)) \(\cup\left\{2\right\}\)
(1) có nghiệm duy nhất trên [2 ; 3] khi
- 4 ≥ - 4m ≥ - 7 ⇔ 1 ≤ m ≤ \(\dfrac{7}{4}\) hay m ∈\(\left[1;\dfrac{7}{4}\right]\)
(1) có nghiệm duy nhất trên [-2; -1] khi
-4 ≤ 4m ≤ 1 hay m ∈ \(\left[\dfrac{-1}{4};1\right]\)
b, (1) có 2 nghiệm phân biệt trên [-2 ; 2] khi
-4m ∈ (-8 ; -7] ⇒ m ∈\(\)[\(\dfrac{7}{4}\); 2)
(1) có 2 nghiệm phân biệt trên [2; 3] và [-2; -1] khi m ∈ ∅
c, (1) có nghiệm trên đoạn
[-2; 2] khi -8 ≤ -4m ≤ 1 ⇒ m ∈ \(\left[\dfrac{-1}{4};2\right]\)
[2 ; 3] khi - 4 ≥ - 4m ≥ - 7 hay m ∈\(\left[1;\dfrac{7}{4}\right]\)
[-2 ; -1] khi -4 ≤ 4m ≤ 1 hay m ∈ \(\left[\dfrac{-1}{4};1\right]\)
d, dường như là nó giống câu b,
e, (1) vô nghiệm trên đoạn [-2 ; 2] khi
\(\left[{}\begin{matrix}-4m>1\\-4m< -8\end{matrix}\right.\)hay \(m\in\left(-\infty;\dfrac{-1}{4}\right)\cup\left(2;+\infty\right)\)
(1) vô nghiệm trên đoạn [2; 3] khi
m ∈ R \ \(\left[1;\dfrac{7}{4}\right]\)
(1) vô nghiệm trên [-2 ; -1] khi m ∈ R \ \(\left[\dfrac{-1}{4};1\right]\)
Có sai sót xin thông cảm
P/s :Bạn tự vẽ bảng biến thiên nha, nhớ chia khoảng cách các giá trị của x cho chuẩn vào, nhớ thêm cả f(0) và trong bảng nhá
