Tính \(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{2n}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 11 2021
\(a,P=\dfrac{1}{\left(2+1\right)\left(2+1-1\right):2}+\dfrac{1}{\left(3+1\right)\left(3+1-1\right):2}+...+\dfrac{1}{\left(2017+1\right)\left(2017+1-1\right):2}\\ P=\dfrac{1}{2\cdot3:2}+\dfrac{1}{3\cdot4:2}+...+\dfrac{1}{2017\cdot2018:2}\\ P=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{2018}\right)=2\cdot\dfrac{504}{1009}=\dfrac{1008}{1009}\)
\(b,\) Ta có \(\dfrac{1}{4^2}< \dfrac{1}{2\cdot4};\dfrac{1}{6^2}< \dfrac{1}{4\cdot6};...;\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{\left(2n-2\right)2n}\)
\(\Leftrightarrow VT< \dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+...+\dfrac{1}{\left(2n-2\right)2n}\\ \Leftrightarrow VT< \dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{\left(2n-2\right)2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2n-2}-\dfrac{1}{2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{2n}\right)< \dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{4}\)
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: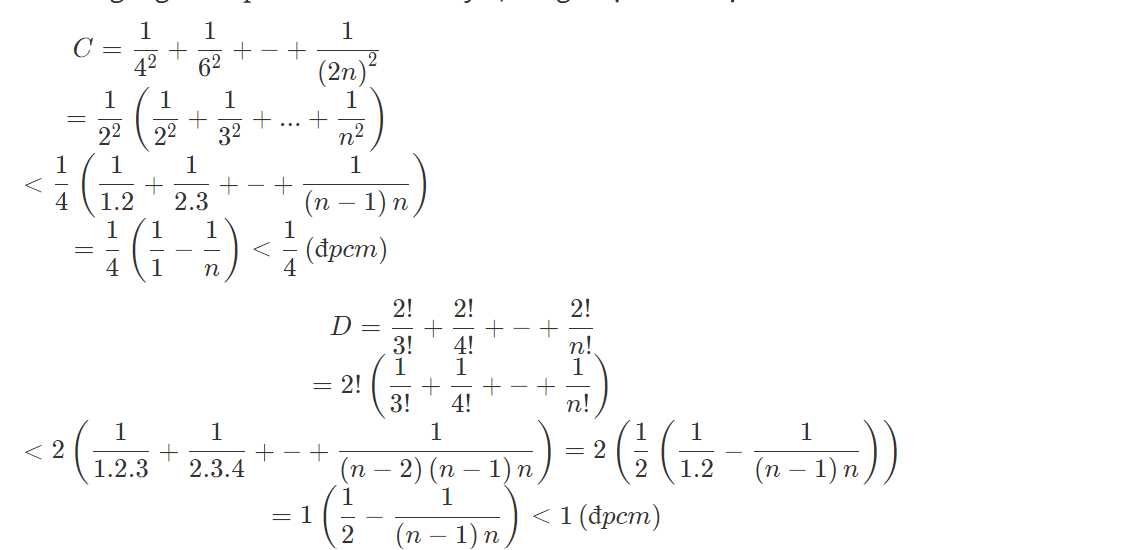 
NB
27 tháng 2 2023
Đặt A=1/2+1/4+1/8+..+1/1024
Ax2=1+1/2+1/4+1/8+..+1/512( Nhân cả 2 vế với 2)
Ax2-A=(1+1/2+1/4+1/8+..+1/512)-(1/2+1/4+1/8+..+1/1024)
<=>A=1-1/1024
<=>A=1023/1024
Vậy biểu thức đã cho = 1023/1024
DT
27 tháng 2 2022
\(a,\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}=\dfrac{8}{16}+\dfrac{4}{16}+\dfrac{2}{16}+\dfrac{1}{16}=\dfrac{8+4+2+1}{16}=\dfrac{15}{16}\)
\(b,\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}=\dfrac{15}{30}+\dfrac{10}{30}+\dfrac{6}{30}=\dfrac{15+10+6}{30}=\dfrac{31}{30}\)
NV
Nguyễn Việt Dũng
CTVVIP
24 tháng 8 2023
a) \(\dfrac{21}{15}\) + \(\dfrac{2}{5}\) = \(\dfrac{9}{5}\)
b) \(\dfrac{6}{16}\) + \(\dfrac{1}{8}\) = \(\dfrac{1}{2}\)
c) \(\dfrac{3}{12}\) + \(\dfrac{3}{4}\) = 1
\(A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{16}-....-\dfrac{1}{2n}\)
\(A=1-\dfrac{1}{2n}\)
\(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{2n}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{n}\)
\(\Rightarrow2A-A=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{n}-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{2n}\right)\)
\(\Rightarrow A=1-\dfrac{1}{2n}\)