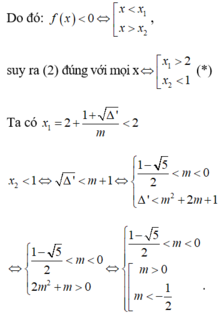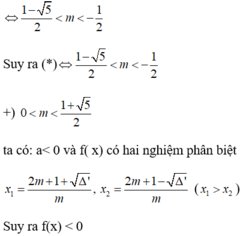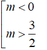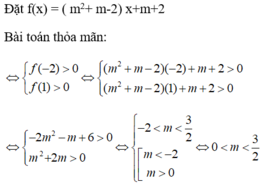Tìm m để bpt: x2 + 3x + 5m + 2 ≥ 0 với mọi x ∈ [-3; +∞]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
HP
4 tháng 3 2021
a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
HP
19 tháng 3 2021
1.
\(2\left|x-m\right|+x^2+2>2mx\)
\(\Leftrightarrow\left(x-m\right)^2+2\left|x-m\right|-m^2+2>0\)
\(\Leftrightarrow t^2+2t-m^2+2>0\left(t=\left|x-m\right|\ge0\right)\)
\(\Leftrightarrow m^2< f\left(t\right)=t^2+2t+2\)
Yêu cầu bài toán thỏa mãn khi \(m^2< minf\left(t\right)=2\)
\(\Leftrightarrow-\sqrt{2}< m< 2\)
Vậy \(-\sqrt{2}< m< 2\)
HP
19 tháng 3 2021
2.
\(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\)
\(\Leftrightarrow\left(x+m\right)^2+2\left|x+m\right|+2m^2-3m+1< 0\)
\(\Leftrightarrow\left(\left|x+m\right|+1\right)^2< -2m^2+3m\)
Ta có \(VT=\left(\left|x+m\right|+1\right)^2=\left(-\left|x+m\right|-1\right)^2\le\left(-1\right)^2=1\)
Yêu cầu bài toán thỏa mãn khi \(VP=-2m^2+3m>1\)
\(\Leftrightarrow2m^2-3m+1< 0\)
\(\Leftrightarrow\dfrac{1}{2}< m< 1\)
HP
23 tháng 5 2022
\(x^2+\left(m-2\right)x-8m\ge0\)
\(\left\{{}\begin{matrix}\Delta\ge0\\x_1+x_2\\x_1x_2\ge0\end{matrix}\right.< 0\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)^2-4\left(-8m\right)\ge0\\-m+2< 0\\-8m\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+4+32m\ge0\\m>2\\m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m+14-8\sqrt{3}\right)\left(m+14+8\sqrt{3}\right)\ge0\\m>2\\m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}\left[{}\begin{matrix}m+14-8\sqrt{3}\ge0\\m+14+8\sqrt{3}\ge0\end{matrix}\right.\\\left[{}\begin{matrix}m+14-8\sqrt{3}\le0\\m+14+8\sqrt{3}\le0\end{matrix}\right.\end{matrix}\right.\\m>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}\left[{}\begin{matrix}m\ge-14+8\sqrt{3}\\m\ge-14-8\sqrt{3}\end{matrix}\right.\\\left[{}\begin{matrix}m\le-14+8\sqrt{3}\\m\le-14-8\sqrt{3}\end{matrix}\right.\end{matrix}\right.\\m>2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge-14+8\sqrt{3}\\m\le-14-8\sqrt{3}\end{matrix}\right.\\m>2\end{matrix}\right.\)
\(\Leftrightarrow m>2\)
Vậy ...
CM
31 tháng 1 2017
Để hàm số nghịch biến với mọi x > 0 thì a < 0 nên 5m + 2 < 0 ⇔ m < − 2 5
Vậy m < − 2 5 thỏa mãn điều kiện đề bài
Đáp án cần chọn là: A
CM
24 tháng 8 2018
Chọn C
Ta có bất phương trình x2- 3x+ 2≤ 0 khi và chỉ khi 1≤ x≤ 2
Yêu cầu bài toán tương đương với bất phương trình:
mx2-2( 2m+1) x+ 5m+3≤0 (1)
có nghiệm x: 1≤ x≤ 2
+ Ta đi tìm m để bất phương trình (1) vô nghiệm trên S
Tức là bpt f( x) = mx2-2( 2m+1) x+ 5m+3< 0 (2)
đúng với mọi x ∈ S
+ Nếu m= 0 (2) trờ thành: -2x+ 3≤0 hay x> 3/2 nên (2) không đúng với mọi x ∈ S
+ Nếu m≠ 0 tam thức f(x) có hệ số a= m, biệt thức ∆’ = -m2+m+ 1
Bảng xét dấu:
VT
0