Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét tam giác EBD và DBC có chung đáy BD
S_EBD = 1/2 S_ABD (đáy ED =1/2 đáy AB) = 1/2 S_BDC (Vì S_ABD = S_BCD vì đều bằng = 1/2 S_ABC)
=> chiều cao đỉnh E đáy BD = 1/2 chiều cao đỉnh C đáy BD
Xét tam giác EKD và DKC có chung đáy DK mà chiều cao đỉnh E = 1/2 chiều cao đỉnh C => S_EKD = 1/2 S_DKC
Mặt khác 2 tam giac này có chung chiều cao hạ từ đỉnh D => đáy KE = 1/2 đáy CK
Vậy KE = 21 : (2+1) = 7 (cm)
CK = 21 - 7 = 14 (cm)
Đáp số:14 cm
a: Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BCDE là tứ giác nội tiếp
hay B,C,D,E cùng thuộc một đường tròn
cho tam giác ABC . trên cạnh BC lấy điểm D sao cho BD= 1/3 BC .nối DE , trên DE lấy điểm G sao cho GD=GE . biết diện tích tam giác AEG = 15 xăng ti mét vuông . tính diện tích tam giác ABC . mình cần gấp giúp mình với
Trên BC lấy G sao cho DG // AC
Dễ dàng suy ra \(\Delta BDG\approx\Delta BAC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{AC}=\frac{DB}{DG}\)(1)
Vì EC // DG nên áp dụng định lý Thalès vào tam giác KDG, ta được:
\(\frac{KE}{KD}=\frac{EC}{DG}\)hay \(\frac{KE}{KD}=\frac{BD}{DG}\)(vì BD = CE (gt)) (2)
Từ (1) và (2) suy ra \(\frac{KE}{KD}=\frac{AB}{AC}\left(đpcm\right)\)
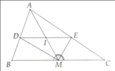
Ta sẽ có S(BEC)=S(BDC) vì cùng bằng 1/2 S(ABC)
tam giác BEC và BCD có chung hình BKC--> S(BEK)=S(DKC)(1)
Kẻ AK ta có S(AEK)=S(BED) (2)và S(AKD)=S(DKC)(3)
Từ 1,2 3 suy 4 tam giác trên bằng nhau
=>S(EAK)=S(AKD)=S(DKC) và S(AEK)= 1/2 S(AKC)
AEK và AKC có chung chiều cao kẻ từ A nên đáy EK=1/2KC
=> EK=1/3 EC=21:3=7 cm
và KE=21-7=14 cm
14 cm đúng rùi đó
do mình làm trong tờ đề học sinh giỏi cấp tỉnh năm 2010 rùi nên biết