Cho x, y, z là ba số dương có tích bằng 1.
Chứng minh rằng: \(\text{(1+ x) (1 + y) (1 + z) ≥ 8}\). Dấu bằng xảy ra khi nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 3 2021
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b\ge2\sqrt{ab}a+b≥2ab ; b+c\ge2\sqrt{bc}b+c≥2bc ; c+a\ge2\sqrt{ca}c+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm.
5 tháng 7 2021
áp dụng bđt cô si ta được
1+x ≥ 2x , 1+y ≥ 2y, 1+z ≥ 2z
Nhân theo vế ba bất đẳng thức này ta được
1+x)(1+y)(1+z)≥ 
\(8\sqrt{xyz}\)
Sử dụng giả thiết ta có đpcm. Đẳng thức xảy ra khi và chỉ khi .
T
16 tháng 9 2018
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1^2}{x}+\frac{1^2}{y}+\frac{1^2}{z}\ge\frac{\left(1+1+1\right)^2}{x+y+z}=\frac{9}{x+y+z}\)( Bất đẳng thức Svac-xơ )
Dấu = xảy ra khi \(\frac{1}{x}=\frac{1}{y}=\frac{1}{z}\)
PN
23 tháng 6 2020
BĐT trên
\(< =>\frac{xy+yz+xz}{xyz}\ge\frac{9}{x+y+z}\)
\(< =>\left(x+y+z\right)\left(xy+yz+xz\right)\ge9xyz\)
Áp dụng BĐT cô si cho 3 số :
\(x+y+z\ge3\sqrt[3]{xyz}\)
\(xy+yz+xz\ge3\sqrt[3]{x^2y^2z^2}\)
Nhân vế với vế : \(\left(x+y+z\right)\left(xy+yz+xz\right)\ge3\sqrt[3]{xyz}.3\sqrt[3]{x^2y^2z^2}=9xyz\)
Nên ta có đpcm
NP
1
4 tháng 6 2023
Ta có \(27=xy+yz+zx\ge3\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow9\ge\sqrt[3]{\left(xyz\right)^2}\) \(\Leftrightarrow729\ge\left(xyz\right)^2\) \(\Leftrightarrow27\ge xyz\) \(\Leftrightarrow27\left(xyz\right)^2\ge\left(xyz\right)^3\) \(\Leftrightarrow\sqrt{3}\sqrt[3]{xyz}\ge\sqrt{xyz}\) (lấy căn bậc 6 2 vế) \(\Leftrightarrow3\sqrt[3]{xyz}\ge\sqrt{3xyz}\)
Do đó \(x+y+z\ge3\sqrt[3]{xyz}\ge\sqrt{3xyz}\). ĐTXR \(\Leftrightarrow x=y=z=3\)
CM
19 tháng 11 2018
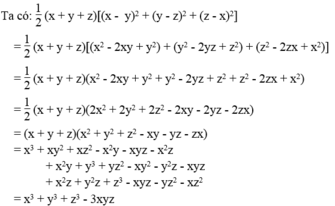
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
M
3
13 tháng 1 2019
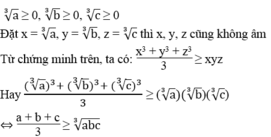
+) Áp dụng BĐT Cô - si cho 4 số dương x; x; y; z ta có:
x+x+y+z≥44√x.x.y.z
=> 2x + y + z ≥44√x.x.y.z (1)
Với 4 số dương 1x ;1x ;1y ;1z ta có: 1x +1x +1y +1z ≥4.4√1x .1x .1y .1z (2)
Từ (1)(2) => (2x+y+z)(1x +1x +1y +1z )≥4.4√x.x.y.z4.4√1x .1x .1y .1z =16
=> 12x+y+z ≤116 .(2x +1y +1z ) (*)
Tương tự, ta có: 1x+2y+z ≤116 .(1x +2y +1z ) (**)
1x+y+2z ≤116 .(1x +1y +2z ) (***)
Từ (*)(**)(***) => Vế trái ≤116 (4x +4y +4z )=14 .(1x +1y +1z )=14 .4=1
=> đpcm
Ta có : \(xyz=1\rightarrow\left\{{}\begin{matrix}xy=\dfrac{1}{z}\\xz=\dfrac{1}{y}\\yz=\dfrac{1}{x}\end{matrix}\right.\)
Do đó : \(A=\left(1+x\right)\left(1+y\right)\left(1+z\right)\)
\(A=1+x+y+z+xy+yz+xz+xyz\)
\(A=1+x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+1\)
\(A=\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)+\left(z+\dfrac{1}{z}\right)+2\)
Áp dụng BĐT \(a+b\ge2\sqrt{ab}\left(a,b>0\right)\)
Dấu \(=\) xảy ra \(\Leftrightarrow a=b\)
với \(x,y,z>0\) Ta được :
\(A\ge2\sqrt{x.\dfrac{1}{x}}+2\sqrt{y.\dfrac{1}{y}}+2\sqrt{z.\dfrac{1}{z}}+2=2+2+2+2=8\)
Dấu \(=\) xảy ra \(\Leftrightarrow\)
\(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\\z=\dfrac{1}{z}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=1\\y^2=1\\z^2=1\end{matrix}\right.\Rightarrow x=y=z=1\) ( vì \(x,y,z>0\) )