Làm hộ em câu rút gọn thui ạ <3
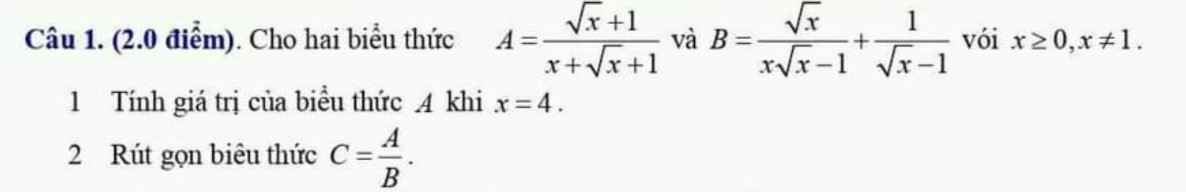
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)

b: B>0
=>\(\dfrac{1}{-x+\sqrt{x}}>0\)
=>\(-x+\sqrt{x}>0\)
=>\(x-\sqrt{x}< 0\)
=>\(\sqrt{x}\left(\sqrt{x}-1\right)< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<x<1

\(A=\left(\sqrt{2}-8\sqrt{32}+2\sqrt{450}\right):\left(-3\sqrt{8}\right)\)
\(=\left(\sqrt{2}-32\sqrt{2}+30\sqrt{2}\right):\left(-6\sqrt{2}\right)\)
\(=\sqrt{2}\left[\left(1-32+30\right):\left(-6\right)\right]\)
\(=\sqrt{2}\left[\left(-1\right):\left(-6\right)\right]\)
\(=\sqrt{2}.\dfrac{1}{6}\)
\(=\dfrac{\sqrt{2}}{6}\)

a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)

a) Trích mẫu thử :
Cho quỳ tím vào 3 mẫu thử :
+ Hóa đỏ : HCl , H2SO4
+ Hóa xanh : KOH
Cho dung dịch BaCl2 vào 2 mẫu thử làm quỳ tím hóa đỏ :
+ Chất nào xuất hiện kết tủa trắng không tan trong axit : H2SO4
Pt : \(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)
Không hiện tượng : HCl
Chúc bạn học tốt
c) Trích mẫu thử :
Cho quỳ tím vào từng mẫu thử :
+ Hóa đỏ : HCl , H2SO4
+ không đổi màu : Na2SO4
Cho dung dịch BaCl2 vào 2 mẫu thử làm quỳ tím hóa đỏ :
+ Chất naò xuất hiện kết tủa trắng không tan trong axit : H2SO4
Pt : \(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)
Không hiện tượng : HCl
Chúc bạn học tốt

16 . ( - 27 ) + 16 . ( - 36 ) + ( - 16 ) . 37
= 16 . ( - 27 ) + 16 . ( - 36 ) + 16 .(-1) .37
=16 . ( - 27 ) + 16 . ( - 36 ) + 16. ( -37)
=16. [ (-27) +(-36) + (-37) ]
=16.(-100)
= -1600
Em chỉ k cho người đầu tiên cos câu trả lời hay và chính xác nhất ạ . Em chân thành cảm ơn nhiều ạ

Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)