cho các số a,b,c khác 0 và thảo mãn b^2=ac. chứng minh a/c=(a+2013b)^2/(b+2013c)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để P(x)=Q(x) thì:\(3x^3+x^2-3x-1=-3x^3-x^2-x-15\)
Nếu \(3x^3+x^2-3x-1=-3x^3-x^2-x-15\)
=>\(\left(3x^3+x^2-3x-1\right)-\left(-3x^3-x^2-x-15\right)=0\)
=>\(3x^3+x^2-3x-1+3x^3+x^2+x+15=0\)
=>\(\left(3x^3+3x^3\right)+\left(x^2+x^2\right)+\left(-3x+x\right)+\left(-1+15\right)=0\)
=>\(6x^3+2x^2-2x+14=0\)
=>\(6x^3+2x^2-2x=-14\)

Vì \(b^2=ac\) ta suy ra \(\dfrac{a}{b}=\dfrac{b}{c}\). Đặt \(a=kb\) và \(b=kc\).
Khi đó \(\dfrac{a}{c}=\dfrac{k\left(kc\right)}{c}=k^2\). (1)
Từ tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{2012b}{2012c}=\dfrac{a+2012b}{b+2012c}=k\), suy ra \(k^2=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\). (2)
Từ (1) và (2) suy ra \(k^2=\dfrac{a}{c}=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\) (đpcm)

Ta có : \(\frac{a}{a+\sqrt{2013a+bc}}=\frac{a}{a+\sqrt{a^2+ab+ac+bc}}=\frac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\)
Theo bất đẳng thức Bunhiacopxki : \(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ab}+\sqrt{ac}\)
\(\Rightarrow\frac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\frac{a}{a+\sqrt{ab}+\sqrt{ac}}=\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
hay \(\frac{a}{a+\sqrt{2013a+bc}}\le\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự : \(\frac{b}{b+\sqrt{2013b+ac}}\le\frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\frac{c}{c+\sqrt{2013c+ab}}\le\frac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng các bất đẳng thức trên theo vế được \(\frac{a}{a+\sqrt{2013a+bc}}+\frac{b}{b+\sqrt{2013b+ac}}+\frac{c}{c+\sqrt{2013c+ab}}\le1\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\\a+b+c=2013\\a,b,c>0\end{cases}}\) \(\Leftrightarrow a=b=c=671\)
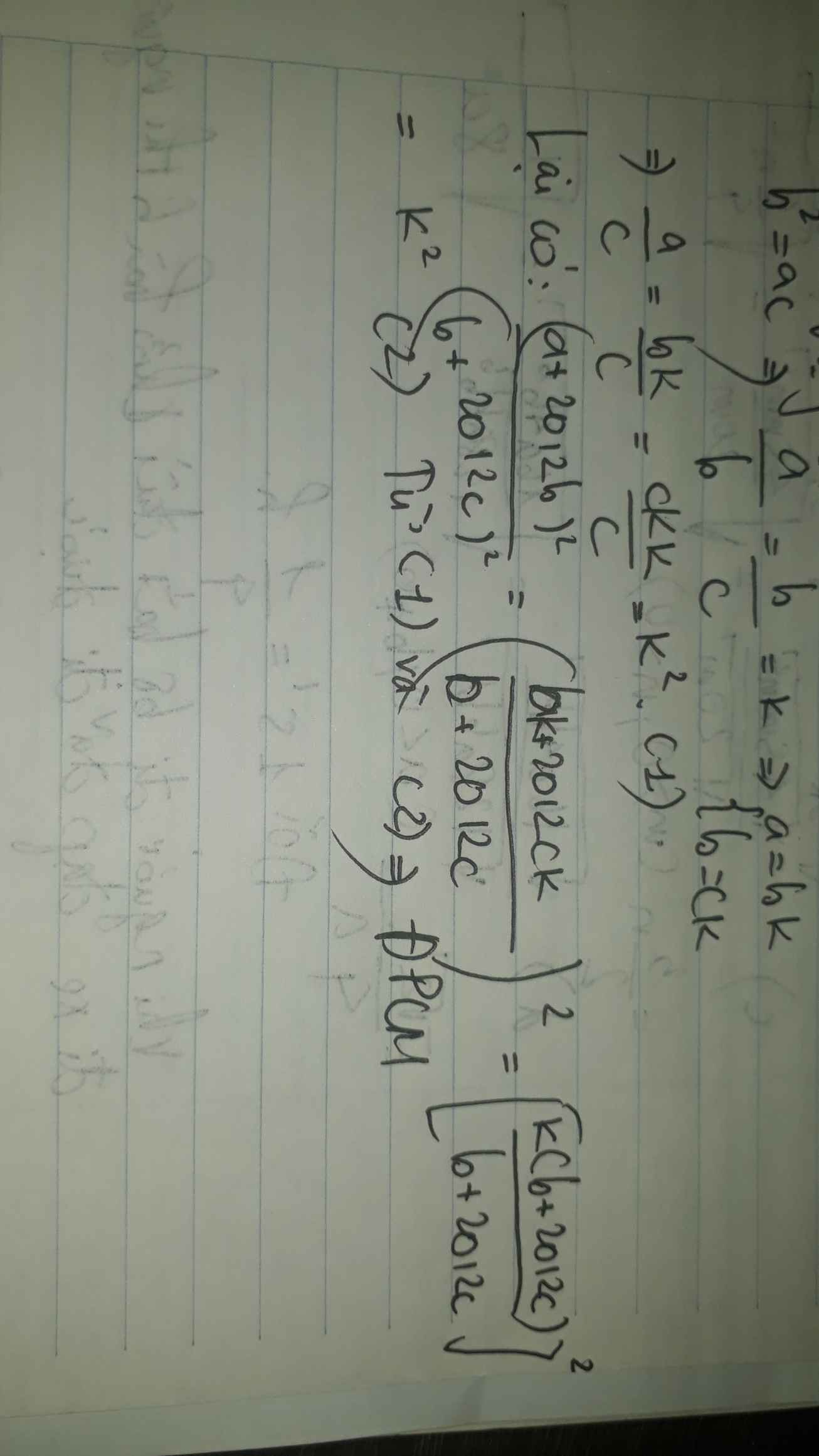
\(b^2=ac\Rightarrow\frac{a}{b}=\frac{b}{c}\)
=> \(\frac{a}{b}=\frac{2013b}{2013c}=\frac{a+2013b}{b+2013c}\)
=> \(\frac{a}{b}.\frac{b}{c}=\frac{a+2013b}{b+2013c}.\frac{a+2013b}{b+2013c}\Rightarrow\frac{a}{c}=\left(\frac{a+2013b}{b+2013c}\right)^2\)
Ta có: \(b^2=a.c\)
Suy ra: \(b.b=a.c\)
Suy ra: \(\frac{a}{b}=\frac{b}{c}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{2013b}{2013c}=\frac{a+2013b}{b+2013c}\)
Khi đó: \(\frac{\left(a+2013b\right)^2}{\left(b+2013c\right)^2}=\left(\frac{a+2013b}{b+2013c}\right)^2=\frac{a}{b}.\frac{b}{c}=\frac{a}{c}\)