các bạn giải chi tiết giúp mình với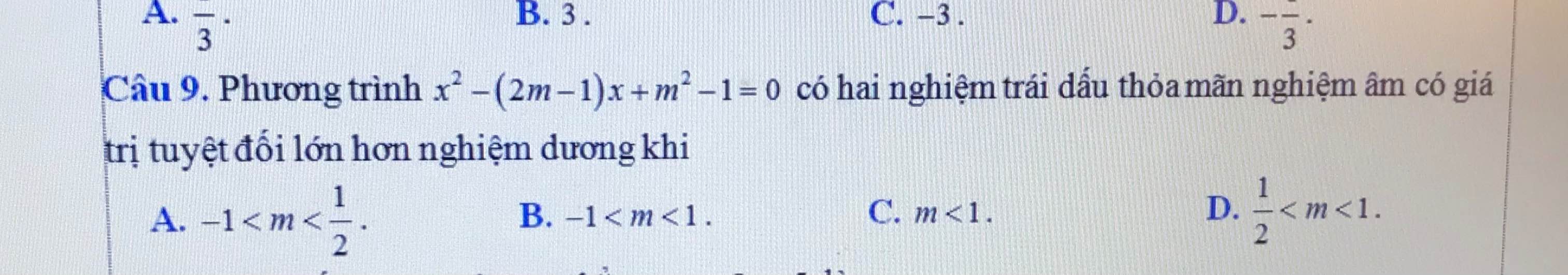
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(\left(\dfrac{1}{2}\cdot x+\dfrac{1}{4}\right)\cdot\left(2x-\dfrac{1}{3}\right)=0\)
\(\dfrac{1}{2}\cdot x+\dfrac{1}{4}=0\)
\(\dfrac{1}{2}\cdot x=0-\dfrac{1}{4}\)
\(\dfrac{1}{2}\cdot x=-\dfrac{1}{4}\)
\(x=-\dfrac{1}{4}\div\dfrac{1}{2}\)
\(x=-\dfrac{1}{2}\)
\(2x-\dfrac{1}{3}=0\)
\(2x=0+\dfrac{1}{3}\)
\(2x=\dfrac{1}{3}\)
\(x=\dfrac{1}{3}\div2\)
\(x=\dfrac{1}{6}\)
\(\Rightarrow\) \(x=\) {\(-\dfrac{1}{2};\dfrac{1}{6}\)}

Lời giải:
a.
Diện tích mảnh đất là: $12.10=120$ (m2)
Diện tích phần đất trồng hoa: $6.8=48$ (m2)
b.
Diện tích trồng cỏ là: $120-48=72$ (m2)
Tổng tiền công chi trả để trồng hoa và cỏ là:
$48.40 000 +72.30 000=4080000$ (đồng)

134/43 = 3,1162... bé - lớn : 55/21 ; 134/43 ; 116/37 ; 74/19
55/21 = 2,6190... lớn - bé : (ngược lại)
74/19 = 3,8947...
116/37 = 3,1351...

a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

\(A=\dfrac{1}{2.3}+\dfrac{1}{4.5}+\dfrac{1}{6.7}+...+\dfrac{1}{18.19}\)
\(< \dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{17.18}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{17}-\dfrac{1}{18}\)
\(=\dfrac{1}{2}-\dfrac{1}{18}=\dfrac{4}{9}=\dfrac{76}{171}< \dfrac{9}{19}=\dfrac{81}{171}\)
\(\Rightarrow A< \dfrac{9}{19}\)

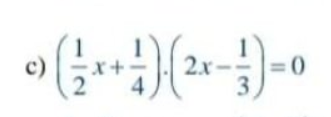

 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)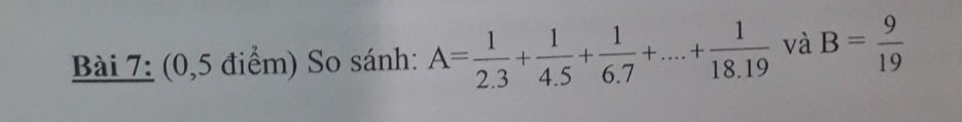
Lời giải:
PT có 2 nghiệm trái dấu khi mà:
\(\left\{\begin{matrix} \Delta=(2m-1)^2-4(m^2-1)=5-4m>0\\ P=m^2-1<0\end{matrix}\right.\Leftrightarrow -1< m< 1\)
Gọi nghiệm dương là $x_1$ và nghiệm âm là $x_2$
Có $x_1+x_2=2m-1$ theo Viet
Theo đề, để $|x_2|> |x_1|$
$\Leftrightarrow -x_2> x_1\Leftrightarrow x_1+x_2<0\Leftrightarrow 2m-1<0$
$\Leftrightarrow m< \frac{1}{2}$
Vậy $-1< m< \frac{1}{2}$
Đáp án A.