
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề 1
Bài 1
a) \(A=\left\{37;38;39;...;91;92\right\}\)
b) \(B=\left\{0;1;2;3;4;5...\right\}\)
Bài 2
a) 210 + 47.84 + 16.47
= 210 + 47.(84 + 16)
= 210 + 47.100
= 210 + 4700
= 4910
b) 53.37 + 53.64 - 57:54
= 53.37 +5 3.64 +5 3
= 53.(37 + 64 - 1)
= 53.100
= 125.100
= 12 500
c) (335 + 334 - 333) : 332
= 335:332 + 334:332 - 333:332
= 33 + 32 - 3
= 27 + 9 - 3
= 33
d) 13 + 16 + 19 + ... + 79 + 82 + 85
25 số hạng
=> Tổng = (85 + 13) x 25:2 = 1225
Bài 3
a) 271 + (x - 86) = 368
x - 86 = 368 - 271
x - 86 = 97
x = 86 + 97
x = 183
b) 2.3x + 4.52= = 154
2.3x+ 100 = 154
2.3x = 154 - 100
2.3x = 54
3x = 54:2
3x = 27
3x = 33
=> x = 3
c) 24x - 3 + 74 = 106
24x - 3 = 106 - 74
24x - 3 = 32
24x - 3 = 25
=> 4x - 3 = 5
4x = 5 + 3
4x = 8
x = 8:4
x = 2
Đề 2
Bài 1
a) \(18.74+18.22+18.4\)
\(=18.\left(74+22+4\right)\)
\(=18.100\)
\(=1800\)
b) \(2016^0+4^4:4^2-5.2\)
\(=1+4^2-10\)
\(=17-10\)
\(=7\)
c) \(40:\left[11+\left(5-2\right)^2\right]\)
\(=40:\left[11+3^2\right]\)
\(=40:\left[11+9\right]\)
\(=40:20\)
\(=2\)
Bài 2
a) \(5.\left(x-13\right)=20\)
\(x-13=20:5\)
\(x-13=4\)
\(x=4+13\)
\(x=17\)
b) \(26-3.\left(x+4\right)=5\)
\(3.\left(x+4\right)=26-5\)
\(3.\left(x+4\right)=21\)
\(x+4=21:3\)
\(x+4=7\)
\(x=7-4\)
\(x=3\)
c) \(12.x-5^4:5^2=35\)
\(12.x-25=35\)
\(12.x=35+25\)
\(12.x=60\)
\(x=60:12\)
\(x=5\)
Bài 3
từ trang 1 đến trang 9 cần số chữ số là : (9-1)+1 *1=9 (chữ số)
từ trang 10 đến trang 99 cần số chữ số là : (99-10)+1 *2 =180 (chữ số)
từ trang 100 đến trang 164 cần số chữ số là : (164-100)+1*3=195 (chữ số)
cân tất cả số chữ số để đánh số trang quyển sách dày 164 trang la : 9+180+195=384 (chữ số)
Đ/S:384 chữ số
Bài 4: 2 + 4 + 6 + ... + 50
Dãy trên có số số hạng là
\(\left(50-2\right):2+1=15\)(số hạng)
Dãy trên nhận giá trị
\(\left(50+2\right)\times15:2=390\)

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3


Từ đề bài ta có:
\(T=\dfrac{1+2}{2}.\dfrac{1+3}{3}.\dfrac{1+4}{4}...\dfrac{1+98}{98}.\dfrac{1+99}{99}\)
\(=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{99}{98}.\dfrac{100}{99}\)
\(=\dfrac{100}{2}\)
\(=50\).
\(T=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)...\left(\dfrac{1}{98}+1\right)\left(\dfrac{1}{99}+1\right)\)
\(T=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}....\dfrac{99}{98}.\dfrac{100}{99}\)
\(T=\dfrac{3.4.5......99}{3.4.5......99}.\dfrac{100}{2}\)
\(T=50\)

Trả lời:
\(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{\left(5x+1\right)\left(5x+6\right)}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5x+1}-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=1-\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=\frac{1}{2006}\)
\(\Rightarrow5x+6=2006\)
\(\Rightarrow5x=2000\)
\(\Rightarrow x=400\)
Vậy x = 400
Trả lời:
\(\frac{x}{2008}-\frac{1}{10}-\frac{1}{15}-\frac{1}{21}-...-\frac{1}{120}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}-\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\right)=\frac{5}{8}\)\(\frac{5}{8}\)
Đặt \(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\), ta được : \(\frac{x}{2008}-A=\frac{5}{8}\) (*)
\(\Rightarrow A=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(\Rightarrow A=2\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{240}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{16}\right)=2.\frac{3}{16}=\frac{3}{8}\)
Thay A vào (*) , ta có:
\(\frac{x}{2008}-\frac{3}{8}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}=1\)
\(\Rightarrow x=2008\)
Vậy x = 2008

a) \(P=2^{100}-2^{99}-2^{98}-...-2^3-2^2-2\)
\(=2^{100}-\left(2+2^2+2^3+...+2^{99}\right)\)
\(A=2+2^2+2^3+...+2^{99}\)
\(2A=2^2+2^3+...+2^{100}\)
\(2A-A=\left(2^2+2^3+...+2^{100}\right)-\left(2+2^2+2^3+...+2^{99}\right)\)
\(A=2^{100}-2\)
\(P=2^{100}-\left(2^{100}-2\right)=2\)


Ta có:
\(\overline{abc}=100.a+10.b+c=n^2-1\) (1)
\(\overline{cba}=100.c+b.10+a=n^2-4n+4\) (2)
Lấy (1) trừ (2) ta được:
\(99\left(a-c\right)=4n-5\)
\(\Rightarrow4n-5⋮99\)
Vì \(100\le\overline{abc}\le999\) nên:
\(100\le n^2-1\le999\)
\(\Rightarrow101\le n^2\le1000\)
\(\Rightarrow11\le31\Rightarrow39\le4n-5\le119\)
Vì \(4n-5⋮99\Rightarrow4n-5=99\Rightarrow n=26\Rightarrow\overline{abc}=675\)
Vậy \(\overline{abc}=675\)
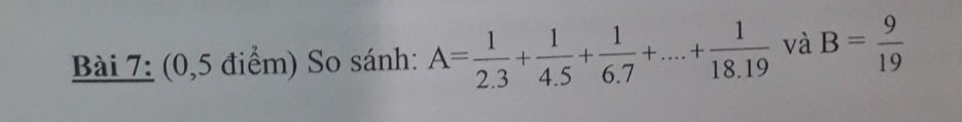



 giải nhanh và chi tiết giúp mình nha
giải nhanh và chi tiết giúp mình nha

 CÁC BẠN GIẢI GIÚP MÌNH NHA! MÌNH ĐANG CẦN GẤP AH
CÁC BẠN GIẢI GIÚP MÌNH NHA! MÌNH ĐANG CẦN GẤP AH giải giùm tớ nha
giải giùm tớ nha

 mình đang cần gấp .các bạn giải nhanh giúp mình với
mình đang cần gấp .các bạn giải nhanh giúp mình với





 Mình cảm ơn ạ
Mình cảm ơn ạ
\(A=\dfrac{1}{2.3}+\dfrac{1}{4.5}+\dfrac{1}{6.7}+...+\dfrac{1}{18.19}\)
\(< \dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{17.18}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{17}-\dfrac{1}{18}\)
\(=\dfrac{1}{2}-\dfrac{1}{18}=\dfrac{4}{9}=\dfrac{76}{171}< \dfrac{9}{19}=\dfrac{81}{171}\)
\(\Rightarrow A< \dfrac{9}{19}\)