cần gấp ạ, trưa mình phải chụp gửi cô rồi,phiền các bạn ghi giả thuyết,kết luận với vẽ hình ạ:((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
1
Những câu hỏi liên quan
16 tháng 6 2023
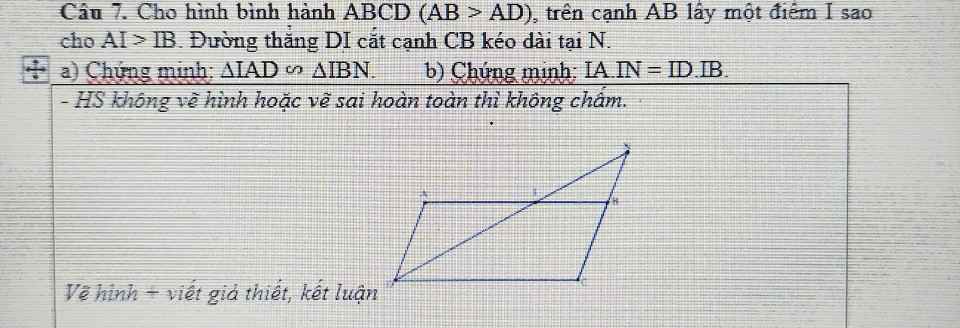
a: Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
b: ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
16 tháng 6 2023
Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
m.người ơi
13 tháng 9 2023
BA=BC
=>góc BAC=góc BCA
=>góc BCA=góc DAC
=>AD//BC
=>ABCD là hình thang
BN
2
11 tháng 5 2021
Bài 5:
a) Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABM=ΔEBM(cạnh huyền-góc nhọn)
11 tháng 5 2021
Bài 5:
b) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc ở đáy)
\(\Leftrightarrow\widehat{MCB}+60^0=90^0\)
hay \(\widehat{MCB}=30^0\)(1)
Ta có: BM là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{MBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(Định lí đảo của tam giác cân)
Suy ra: MB=MC(Hai cạnh bên)
Xét ΔMBE vuông tại E và ΔMCE vuông tại E có
MB=MC(cmt)
ME chung
Do đó: ΔMBE=ΔMCE(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CE(Hai cạnh tương ứng)
10 tháng 1 2023
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
a: XétΔOIA và ΔOIB có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOIA=ΔOIB
b: ta có: ΔOAB cân tại O
mà OI là đường phân giác
nên OI là đường cao
c: Xét ΔONI vuông tại N và ΔOMI vuông tại M có
OI chung
\(\widehat{NOI}=\widehat{MOI}\)
Do đó: ΔONI=ΔOMI
Suy ra: IN=IM