Cho hình chữ nhật MNPQ (MN>NP) kẻ MN vuông QN={H}. a.CM:∆MNH~∆NQP. b.CM:MN^2=QN.NH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

31 tháng 3 2021
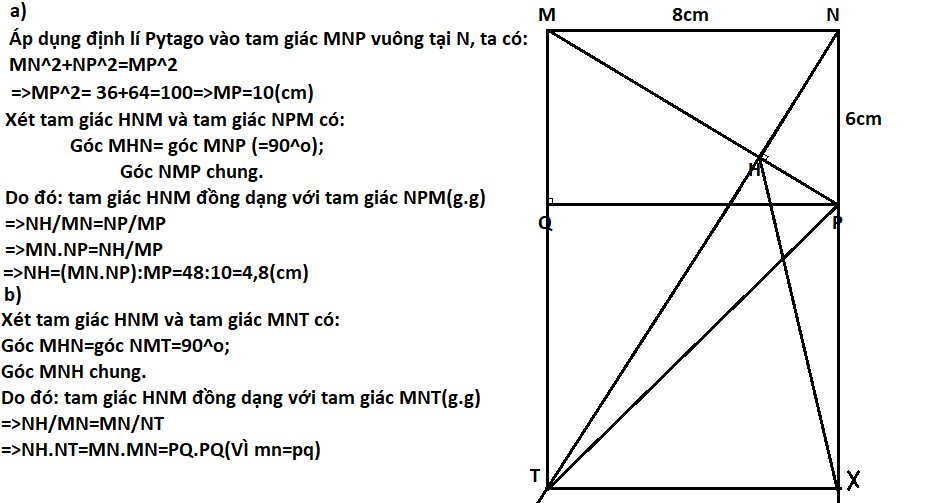
a) Xét ΔMNH vuông tại H và ΔNQP vuông tại P có
\(\widehat{MNH}=\widehat{NQP}\)(hai góc so le trong, MN//QP)
Do đó: ΔMNH\(\sim\)ΔNQP(g-g)
31 tháng 3 2021
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔMNQ vuông tại M có MH là đường cao ứng với cạnh huyền NQ, ta được:
\(NH\cdot NQ=MN^2\)

13 tháng 3 2023
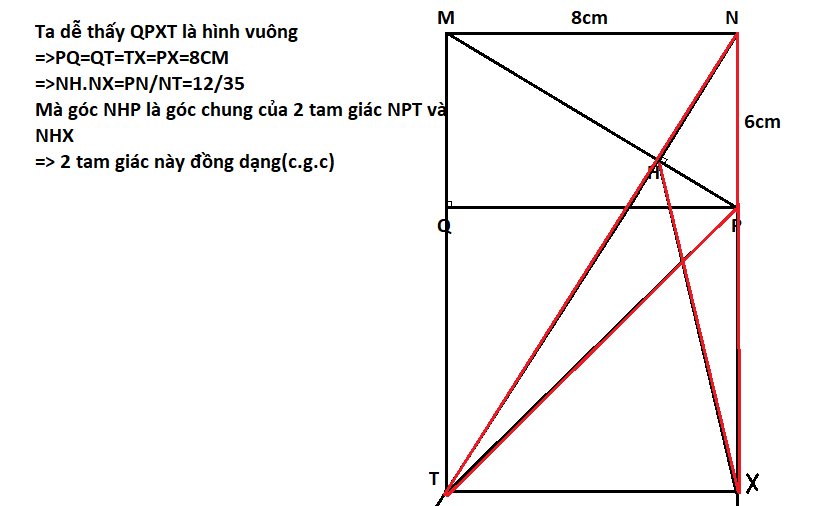
1: Xét ΔMHN vuong tại H và ΔNPQ vuông tại P có
góc MNH=góc NQP
=>ΔMHN đồng dạng với ΔNPQ
2: EQ/EN=PQ/PN=HN/MH
=>EQ*MH=EN*HN
a: Xét ΔMNH vuông tại H và ΔNQP vuông tại P có
\(\widehat{MNH}=\widehat{NQP}\)
Do đó: ΔMNH\(\sim\)ΔNQP
b: Xét ΔMNQ vuông tại M có MH là đường cao
nên \(MN^2=NH\cdot NQ\)