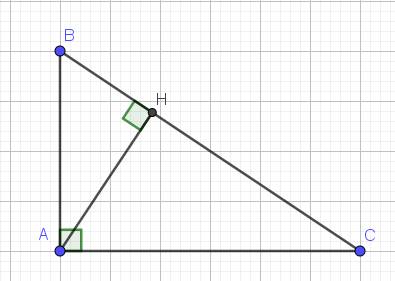
Cho\(\Delta ABC\)vuông tại A có đường cao AH.Dùng định lí Pi-ta-go và diện tích tam giác (ko dùng tam giác đồng dạng) để chứng minh các hệ thức lượng (lớp 9) sau :
a) HB.HC = AH2
b) HB.BC = AB2 => HC.BC = AC2
c)\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)



Phần c đơn giản lắm :) Vừa nghĩ ra tiếp :
Ta có :
\(\Rightarrow\left(AB.AC\right)^2=\left(AH.BC\right)^2\)
\(\Rightarrow AB^2.AC^2=AH^2.BC^2\)
Mà \(BC^2=AB^2+AC^2\)( Pythagores )
\(\Rightarrow AB^2.AC^2=AH^2\left(AB^2+AC^2\right)\)
\(\Rightarrow\frac{1}{AH^2}=\frac{AB^2+BC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
Vậy...
Ngồi nháp rồi nghĩ ra phần a :) Sẽ cập nhật khi nghĩ được b , c
[ Tự vẽ hình ]
Áp dụng định lý Pythagores có :
\(\Rightarrow AH^2=\frac{AC^2-HC^2+AB^2-HB^2}{2}\)
\(=\frac{\left(AB^2+AC^2\right)-\left(HB^2+HC^2+2HB.HC\right)+2HB.HC}{2}\)
\(=\frac{BC^2-\left(HB+HC\right)^2+2HB.HC}{2}\)
\(=\frac{BC^2-BC^2+2HB.HC}{2}\)
\(=\frac{2HB.HC}{2}\)
\(=HB.HC\)
Vậy \(AH^2=HB.HC.\)