Cho đường tròn \(\left(O;AB=2R\right)\). Lấy C là một điểm trên đường tròn để \(AC>BC\). Vẽ hình vuông ACDE có D thuộc tia tia đối của tia BC. CE cắt đường tròn tại F (F không trùng C). Qua A, kẻ tiếp tuyến cắt BF tại H. Chứng minh rằng D, E, H thẳng hàng.
*Giải bằng cách xét 2 tam giác AEH và ACB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔODE cân tại O
mà OM là trung tuyến
nên OM vuông góc DE
=>góc OMA=90 độ=góc OCA=góc OBA
=>O,A,B,M,C cùng thuộc 1 đường tròn
b: Xét ΔBSC và ΔCSD có
góc SBC=góc SCD
góc S chung
=>ΔBSC đồng dạng với ΔCSD
=>SB/CS=SC/SD
=>CS^2=SB*SD
góc DAS=gócEBD
=>góc DAS=góc ABD
=>ΔSAD đồng dạng với ΔSBA
=>SA/SB=SD/SA
=>SA^2=SB*SD=SC^2
=>SA=SC
c; BE//AC
=>EH/SA=BH/SC=HJ/JS
mà SA=SC
nênHB=EH
=>H,O,C thẳng hàng

có góc AQB= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O) Hay góc AQP=90 độ => góc QAP= 90 độ- góc QPA=90 độ-1/2sđ cung AP
có góc APC= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O1)=> góc PAC=90 độ - góc PCA=90 độ - 1/2sđ cung AP
Vì vậy góc QAP= góc PAC hay AP là tia phân giác của góc QAB
Ta có: góc BQA =90o (góc nội tiếp chắn nửa (O))
Xét Δ PQA vuông tại Q có: góc QAP + góc QPA =90o ⇒ góc QAP=90o- góc QPA
Mà góc QPA =1/2 sđ cung PA ( góc QPA là góc tạo bởi tia tiếp tuyến cà dây cung chắn cung AP của (O1))
⇒góc QAP=90o- 1/2 sđ cung PA (1)
Xét ΔCPA vuông tại P ( vì góc CPA là góc nội tiếp chắn nửa (O1)) có
góc PCA + góc PAC =90o⇒góc PAC =90o-góc PCA
mà góc PCA =1/2 sđ cung PA ( góc nội tiếp chắn cung PA )
⇒góc PAC= 90o-1/2 sđ cung PA (2)
Từ (1) và (2) ⇒ góc QAP=góc PAC ⇒ AP là tia phân giác của góc QAB

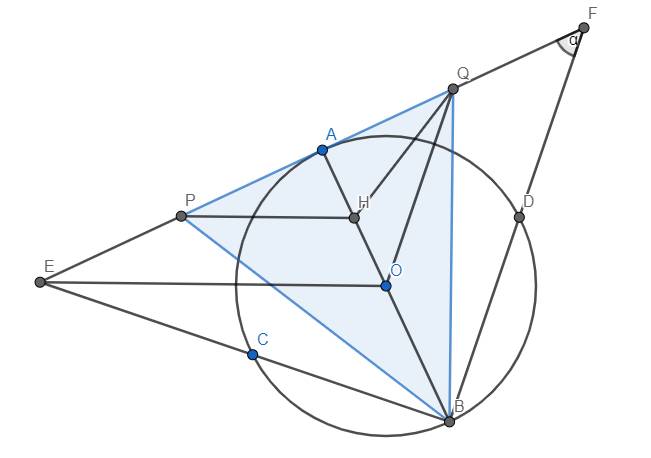
a) Định nghĩa lại H là trung điểm OA. Ta thấy OQ là đường trung bình của tam giác ABF nên OQ//BF. Hơn nữa \(BF\perp BE\) nên \(OQ\perp BE\). Lại có \(BA\perp QE\) nên O là trực tâm của tam giác BEQ \(\Rightarrow OE\perp BQ\)
Mặt khác, PH là đường trung bình của tam giác AOE nên PH//OA. Do đó, \(PH\perp BQ\). Lại thấy rằng \(BH\perp PQ\) nên H là trực tâm tam giác BPQ (đpcm)
b) Ta có \(P=\sin^6\alpha+\cos^6\alpha\)
\(=\left(\sin^2\alpha\right)^3+\left(\cos^2\alpha\right)^3\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)\left(\sin^4\alpha+\cos^4\alpha-\sin^2\alpha\cos^2\alpha\right)\)
\(=1.\left[\left(\sin^2\alpha+\cos^2\alpha\right)^2-3\sin^2\alpha\cos^2\alpha\right]\)
\(=1-3\sin^2\alpha\cos^2\alpha\)
\(\le1-3.\dfrac{\left(\sin^2\alpha+\cos^2\alpha\right)^2}{4}\)
\(=\dfrac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\sin\alpha=\cos\alpha\) \(\Leftrightarrow\alpha=45^o\) hay 2 dây AB, CD vuông góc với nhau.
Vậy \(min_P=\dfrac{1}{4}\)
c) Ta có \(\left\{{}\begin{matrix}EC.EB=EA^2\\FD.FB=FA^2\end{matrix}\right.\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow EC.EB.FD.FB=\left(EA.FA\right)^2\)
\(\Rightarrow EC.FD.\left(EB.DB\right)=AB^4\)
\(\Rightarrow EC.FD.\left(EF.AB\right)=AB^4\)
\(\Rightarrow EC.FD.EF=AB^3=CD^3\) (đpcm)
Ta có \(EC.DF=AC.AD=BC.BD\)
\(\Rightarrow\dfrac{EC}{DF}=\dfrac{BC.BD}{DF^2}\)
\(=\dfrac{BC}{DF}.\dfrac{BD}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AC}{DF}\)
\(=\dfrac{BE}{BF}.\dfrac{AE}{AF}\)
\(=\left(\dfrac{BE}{BF}\right)^3\)
Ta có đpcm.
Bài khá căng đấy


a) Xét 2 tam giác ABE và ACF, ta có:
\(\widehat{AEB}=\widehat{ACF}=90^o\) và \(\widehat{A}\) chung
nên \(\Delta ABE~\Delta ACF\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\) \(\Rightarrow AB.AF=AC.AE\) (đpcm)
b) Từ \(AB.AF=AC.AE\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\). Từ đó dễ dàng chứng minh \(\Delta AEF~\Delta ABC\left(c.g.c\right)\)
c) Kẻ đường kính AP của (O). Ta có \(\left\{{}\begin{matrix}AB\perp BP\\AB\perp HC\end{matrix}\right.\) \(\Rightarrow\) BP//HC
CMTT, ta có CP//HB, dẫn đến tứ giác BHCP là hình bình hành. Lại có A' là trung điểm BC \(\Rightarrow\) A' cũng là trung điểm HP.
Do đó OA' là đường trung bình của tam giác PAH \(\Rightarrow AH=2A'O\left(đpcm\right)\)

a) Xét 2 TH:
- TH \(P_x,P_y\) nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)
Kẻ \(OI\perp P_x\) ta có:
\(IP=IE,IA=IB\)
\(\Rightarrow PI-AI=EI-BI\) hay PA=BE ( đpcm)
b) Kẻ \(OK\perp P_y\)
Trong đường tròn \(\left(O;r\right)\), vì AB>CD => OI<OK
Khi đó trong đường tròn \(\Rightarrow PE>PF\)
Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn \(\left(O;R\right)\)
ta có: cung PE > cung PF ( đpcm)
Giải :
a) kẻ OH vuông góc với PE bà AB
⇒ H là trđ PE, AB
hay HP = HE, HA = HB
⇒ HP - HA = HE - HB
⇒ AP = BE.
b) kẻ OK vuông góc với PF
-Xét (O;r) có : AB > CD ( gt)
⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )
-Xét (O;R) có : OH < OK (cmt )
⇒ PE> PF.
