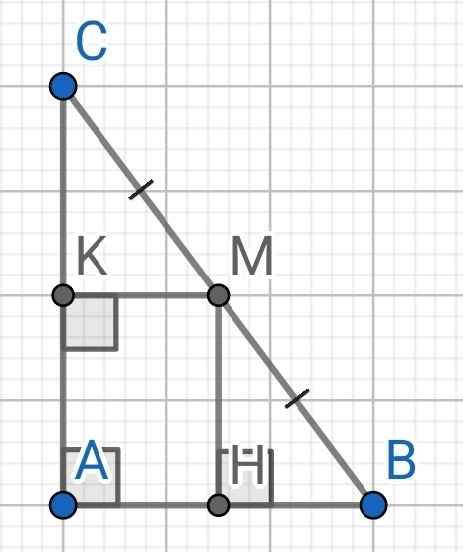
cho tam giác ABC vuông cân tại A. Gọi M là một điểm trên BC. Vẽ MH vuông góc với AB, MKvuông góc với AC. Cho AB = 4 cm. AHMK là hình gì ? Tính chu vi AHMK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề: vẽ MH\(\perp\)AB, MK\(\perp\)AC
Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
=>AHMK là hình chữ nhật
b: Vì ΔABC vuông tại A
nên \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)
\(=\dfrac{1}{2}\cdot6\cdot8=\dfrac{1}{2}\cdot48=24\left(cm^2\right)\)

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó; AHMK là hình chữ nhật

a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật

 a) Do MH ⊥ AB (gt)
a) Do MH ⊥ AB (gt)
⇒ ∠AHM = 90⁰
Do MK ⊥ AC (gt)
⇒ ∠AKM = 90⁰
Tứ giác AHMK có:
∠AHM = ∠HAK = ∠AKM = 90⁰
⇒ AHMK là hình chữ nhật
b) AB = AC (gt)
⇒ ∆ABC vuông cân tại A
AM là đường trung tuyến
⇒ AM cũng là đường phân giác của ∆BAC
⇒ AM là đường phân giác của ∠HAK
Ta có:
AHMK là hình chữ nhật (cmt)
AM là đường phân giác của ∠HAK (cmt)
⇒ AHMK là hình vuông

a: Xét tứ giác AHMK có
góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hình chữ nhật
b: Xet ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
c: Xét tứ giác AMCN có
K là trung điểm chung của AC và MN
MA=MC
Do đó: AMCN là hình thoi
