Tìm x biết
5x + 5x+2 =650
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5x+5x^2=43x^3\\ \Rightarrow43x^3-5x^2-5x=0\\ \Rightarrow x\left(43x^2-5x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\43x^2-5x-5=0\left(1\right)\end{matrix}\right.\\ \Delta\left(1\right)=25+4.5.43=885\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5+\sqrt{885}}{86}\\x=\dfrac{5-\sqrt{885}}{86}\end{matrix}\right.\)



a, x - 3 : 2 = 5 14 : 5 12
=> x - 3 : 2 = 5 2
=> x - 3 : 2 = 25
=> x – 3 = 25
=> x = 53
b, 30 : x - 7 = 15 19 : 15 18
=> 30 : x - 7 = 15
=> x – 7 = 2
=> x = 9
c, x 70 = x
=> x 70 - x = 0
=> x ( x 69 - 1 ) = 0
=> 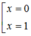
d, 2 x + 1 3 = 9 . 81
=> 2 x + 1 3 = 9 3
=> 2x + 1 = 9
=> x = 4
e, 5 x + 5 x + 2 = 650
=> 5 x 1 + 5 2 = 650
=> 5 x . 26 = 650
=> 5 x = 25
=> x = 2
f, 4 x - 1 2 = 25 . 9
=> 4 x - 1 2 = 5 2 . 3 2
=> 4 x - 1 2 = 15 2
=> 4x – 1 = 15
=> x = 4

a) \(5^2\cdot3^x=575\)
\(\Rightarrow3^x=\dfrac{575}{5^2}\)
\(\Rightarrow3^x=\dfrac{575}{25}\)
\(\Rightarrow3^x=23\)
Xem lại đề
b) \(5\cdot2^x-7^2=31\)
\(\Rightarrow5\cdot2^x=31+49\)
\(\Rightarrow5\cdot2^x=80\)
\(\Rightarrow2^x=\dfrac{80}{5}\)
\(\Rightarrow2^x=16\)
\(\Rightarrow2^x=2^4\)
\(\Rightarrow x=4\)
c) \(5^x+5^{x+2}=650\)
\(\Rightarrow5^x\cdot\left(1+5^2\right)=650\)
\(\Rightarrow5^x\cdot26=650\)
\(\Rightarrow5^x=\dfrac{650}{26}\)
\(\Rightarrow5^x=25\)
\(\Rightarrow5^x=5^2\)
\(\Rightarrow x=2\)
a, 52 x \(3^x\) = 575
3\(^x\) = 575 : 52
3\(^x\) = 23
nếu \(x\) ≤ 0 ta có 3\(^x\) ≤ 1 < 23 (loại) (1)
Nếu \(x\) ≥ 1 ⇒ 3\(^x\) ⋮ 3 \(\ne\) 23 vì 23 không chia hết cho 3 (2)
kết hợp (1) và(2) ta thấy không có giá trị nào của \(x\) thỏa mãn đề bài
Kết luận: \(x\in\varnothing\)

TK :
5x + 5x +2 = 650
5x + 5x . 52 = 650
5x .( 1 +25 ) = 650
5x .26 = 650
5x = 650 / 26 =25
5x = 52
nên x=2
thiếu bn ơi
BẠN ƠI BẠN CÓ GHI THIẾU ĐỀ K