Cho tam giác ABC có 3 góc nhọn, các đường cao BH và CK
a) CMR: Tam giác AHB và AKC đồng dạng.
b) Tính góc AHK biết góc ABC=58 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 3 2022
Xét tam giác AHB và tam giác AKC
^A _ chung ; AB = AC
Vậy tam giác AHB = tam giác AKC (ch-gn)
=> AH/AK = AB/AC => AH/AB = AK/AC
Xét tam giác AKH và tam giác ACB có
^A _ chung; AH/AB = AK/AC
Vậy tam giác AKH ~ tam giác ACB (c.g.c)
1 tháng 4 2023
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiêp
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét ΔDAB vuông tại D và ΔDCH vuông tại D có
góc DAB=góc DCH
=>ΔDAB đồng dạng vơi ΔDCH
=>DA/DC=DB/DH
=>DA*DH=DB*DC
c: Xét ΔHDC vuông tại D và ΔHFA vuông tại F có
góc DHC=góc FHA
=>ΔHDC đồng dạng vơi ΔHFA
=>HD/HF=HC/HA
=>HF*HC=HD*HA
Xet ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE=HD*HA
23 tháng 4 2016
vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)
QV
1 tháng 8 2016
a)Gọi giao của đường phân giác góc BAC và đường thẳng HK là E
Xét ΔAHK có AE vừa là đường cao vừa là đường phân giác
⇒ΔAHK cân tai A
B) vẽ đoạn thẳng BC′//HKđễ thấy AB=AC Mặt khác ΔAHK cân tại A nên AH=AK⇒BH=C′K lại có D là trung điểm BC và HK qua D, song song với BC′ nên DK là đường trung bình của ΔBCC′⇒K là trung điểm CC′⇒CK=C′K⇒BH=CK′
Phần c mk k pít lm nha
nhớ click đúng cho mk
16 tháng 3 2020
Tham khảo link này : https://olm.vn//hoi-dap/detail/244303790856.html?auto=
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 4 2023
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
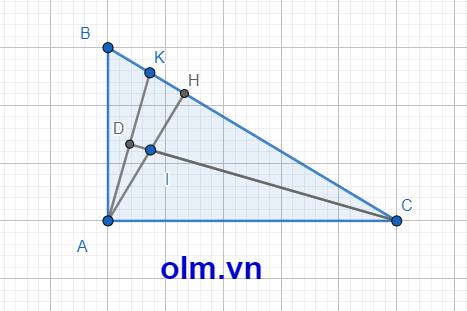
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)
20 tháng 1 2022
a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABC}\) chung
Do đó; ΔAHB\(\sim\)ΔCAB
Suy ra: AB/CB=HB/AB
hay \(AB^2=HB\cdot BC\)
b: BC=25cm
BH=225:25=9(cm)
CH=25-9=16(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
a, Xét tam giác AHB và tam giác AKC ta có
^AHB = ^AKC = 900
^A _ chung
Vậy tam giác AHB ~ tam giác AKC ( g.g )
\(\Rightarrow\frac{AH}{AK}=\frac{AB}{AC}\Rightarrow\frac{AC}{AK}=\frac{AB}{AH}\)
b, Xét tam giác AHK và tam giác ABC ta có :
^A _ chung
\(\frac{AC}{AK}=\frac{AB}{AH}\)( cmt )
Vậy tam giác AHK ~ tam giác ABC ( c.g.c )
Do 2 tam giác đồng dạng theo trường hợp c.g.c tức là ^AHK = ^ABC
mà ^ABC = 580 => ^AHK = 580