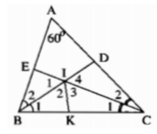
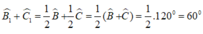Cho \(\Delta ABC\)có góc A = 60o kẻ BD , CE là các tia phân giác của các góc B , C (D \(\varepsilon\)AC, E\(\varepsilon\)AB). BD và CE cắt nhau tại I . Kẻ tia phân giác của góc BIC (F \(\varepsilon\)BC). Chứng minh rằng:
\(-\)\(\Delta BEI=\Delta BFI\)
\(-\)BE+CD=BC
\(-\)ID=IE=IF
GIÚP MK VS , CÁC BN CHỈ CẦN LÀM HAI Ý SAU LÀ ĐC RỒI