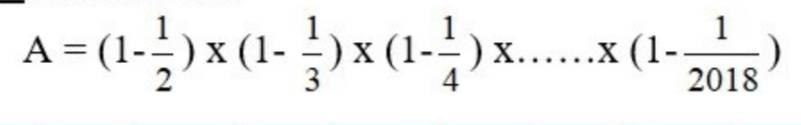 giúp mình với ét o ét
giúp mình với ét o ét
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\alpha\in\left(-90;0\right)\Rightarrow\left\{{}\begin{matrix}sina< 0\\cosa>0\end{matrix}\right.\) \(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{3}{5}\)
\(cot\left(a+60^0\right)=\dfrac{cos\left(a+60^0\right)}{sin\left(a+60^0\right)}=\dfrac{cosa.cos60^0-sina.sin60^0}{sina.cos60^0+cosa.sin60^0}\)
\(=\dfrac{\dfrac{3}{5}.\dfrac{1}{2}-\left(-\dfrac{4}{5}\right).\dfrac{\sqrt{3}}{2}}{-\dfrac{4}{5}.\dfrac{1}{2}+\dfrac{3}{5}.\dfrac{\sqrt{3}}{2}}=...\)
\(sin\left(45^0-a\right)=sin45^0.cosa-cos45^0.sina=\dfrac{\sqrt{2}}{2}.\dfrac{3}{5}-\dfrac{\sqrt{2}}{2}.\left(-\dfrac{4}{5}\right)=...\)

Câu 9: A
Câu 10: C
Câu 11: C
Câu 12: A
Câu 13; B
Câu 14: C

Nhóm 1: Từ ghép phân loại:
-Máy bay, Bánh nếp, Đồng lúa
Nhóm 2: Từ ghép tổng hợp:
- Núi non, Bánh trái, Đồng ruộng, Màu xanh, Màu sắc.
Nhóm 1: Từ ghép phân loại:
-Máy bay, Bánh nếp, Đồng lúa
Nhóm 2: Từ ghép tổng hợp:
- Núi non, Bánh trái, Đồng ruộng, Màu xanh, Màu sắc.

a. Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD\in\left(SCD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
b.
E là trung điểm AB, F là trung điểm CD \(\Rightarrow EF||AD\Rightarrow EF\perp AB\)
Lại có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp EF\Rightarrow EF\perp\left(SAB\right)\)
\(\Rightarrow\left(SAB\right)\perp\left(SEF\right)\) (1)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\\SA\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow\left(SAB\right)\perp\left(ABCD\right)\) (2)
(1);(2) \(\Rightarrow\widehat{SEA}\) là góc giữa (SEF) và (ABCD)
\(AE=\dfrac{1}{2}AB=\dfrac{a}{2}\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=2\sqrt{2}\)
c.
\(BC||AD\Rightarrow BC||\left(AHD\right)\Rightarrow d\left(C;\left(AHD\right)\right)=d\left(BC;\left(AHD\right)\right)=d\left(M;\left(AHD\right)\right)\)
Gọi N là giao điểm AM và EF.
Do EF là đường trung bình của hình chữ nhật ABCD \(\Rightarrow N\) là trung điểm AM
H là trung điểm SM, N là trung điểm AM \(\Rightarrow HN\) là đường trung bình tam giác SAM
\(\Rightarrow HN||SA\Rightarrow HN\perp\left(ABCD\right)\)
\(\left\{{}\begin{matrix}MN\cap\left(HAD\right)=A\\MA=2NA\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(AHD\right)\right)=2d\left(N;\left(AHD\right)\right)\)
Trong mp (ABCD), từ N kẻ \(NP\perp AD\)
Trong mp (HNP), từ N kẻ \(NQ\perp HP\)
\(\Rightarrow NQ\perp\left(AHD\right)\Rightarrow NQ=d\left(N;\left(AHD\right)\right)\)
\(HN=\dfrac{1}{2}SA=\dfrac{a\sqrt{2}}{2}\) ; \(NP=AE=\dfrac{a}{2}\)
Hệ thức lượng trong tam giác vuông HNP:
\(NQ=\dfrac{HN.NP}{\sqrt{HN^2+NP^2}}=\dfrac{a\sqrt{6}}{6}\)
\(\Rightarrow d\left(C;\left(AHD\right)\right)=2NQ=\dfrac{a\sqrt{6}}{3}\)



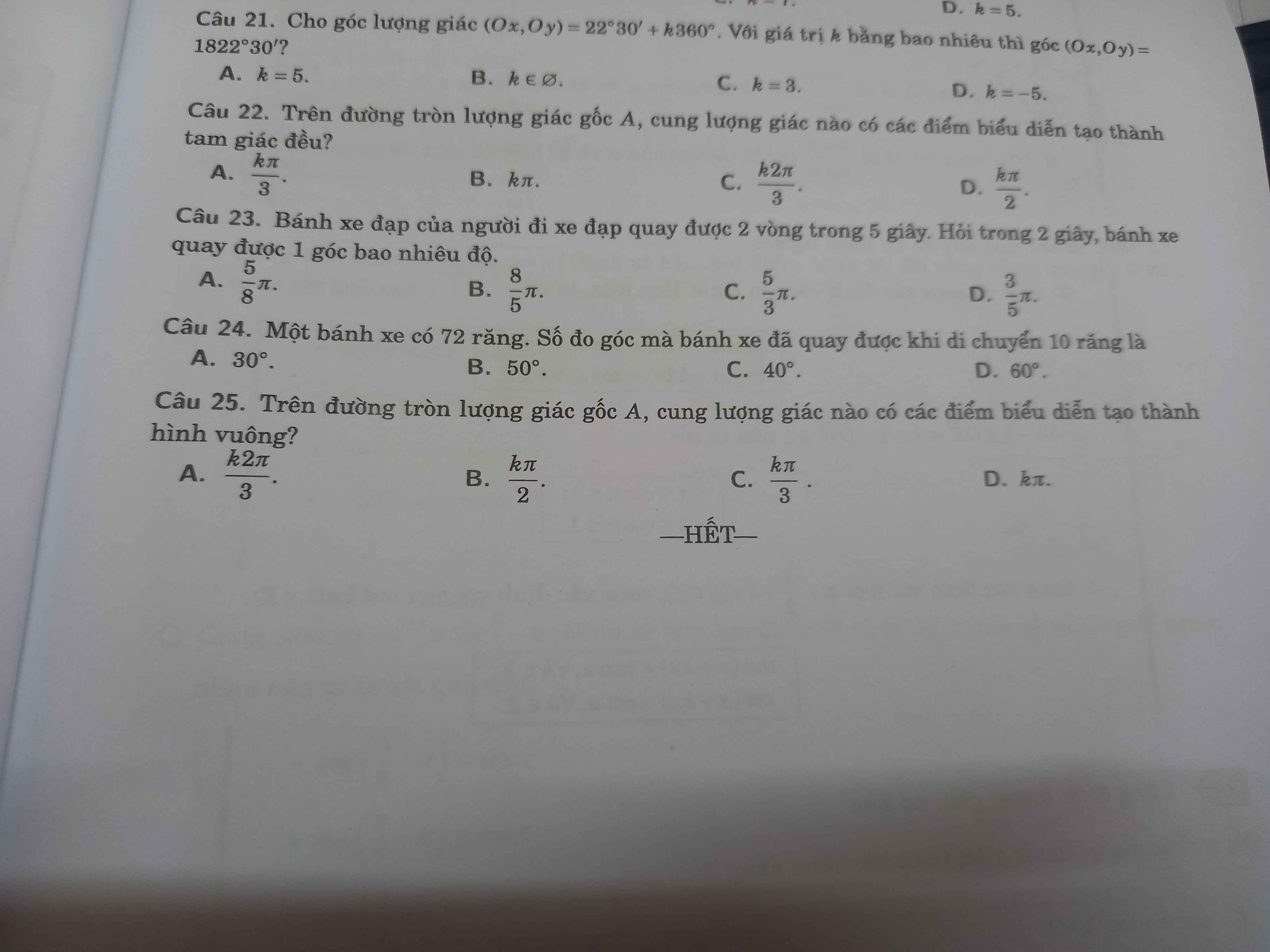
 giúp với ét o ét
giúp với ét o ét
\(A=\dfrac{1.2.3...2017}{2.3.4...2018}=\dfrac{1}{2018}\)