cho tam giác ABC vuông tại A. lấy điểm M bất kì trên cạnh AB(M khác A và B),từ M vẽ đg thẳng vuông góc với BC tại N
a)chứng minh BMN đồng dạng tam giác BCA
b) chứng minh BM×BA=BN×BC
c)gọi EF lần lượt là trung điểm của AN và CN. chứng minhh góc ABE = góc CBF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 5 2022
a) -△DBE và △ACE có: \(\widehat{BDE}=\widehat{CAE};\widehat{BEC}\) là góc chung.
\(\Rightarrow\)△DBE∼△ACE (g-g).
b) △DBE∼△ACE \(\Rightarrow\dfrac{EB}{EC}=\dfrac{ED}{EA}\Rightarrow\dfrac{EB}{ED}=\dfrac{EC}{EA}\)
-△EAD và △ECB có: \(\dfrac{EB}{ED}=\dfrac{EC}{EA};\widehat{BEC}\) là góc chung.
\(\Rightarrow\)△EAD∼△ECB (c-g-c) nên \(\widehat{EAD}=\widehat{ECB}\)
c) EM cắt BC tại F.
-△BCE có: 2 đường cao BD và CA cắt nhau tại M.
\(\Rightarrow\)M là trực tâm của △BCE.
\(\Rightarrow\)EM⊥BC tại F.
-△BMF và △BCD có: \(\widehat{DBC}\) là góc chung, \(\widehat{BFM}=\widehat{BDC}=90^0\).
\(\Rightarrow\)△BMF∼△BCD (g-g).
\(\Rightarrow\dfrac{BM}{BC}=\dfrac{BF}{BD}\Rightarrow BM.BD=BC.BF\left(1\right)\)
-△CMF và △CBA có: \(\widehat{CFM}=\widehat{CAB}=90^0,\widehat{CBA}\) là góc chung.
\(\Rightarrow\)△CMF∼△CBA (g-g).
\(\Rightarrow\dfrac{CM}{CB}=\dfrac{CF}{CA}\Rightarrow CM.CA=CB.CF\left(2\right)\)
-Từ (1) và (2) suy ra:
\(BM.BD+CM.CA=BC.BF+CB.CF=BC\left(BF+CF\right)=BC.BC=BC^2\)
không đổi.
19 tháng 5 2016
a) tam giác BAC vuông tại A và tam giác BMN vuong tại M có: góc BAC=góc BMN
=> tam giác BAC đồng dạng tam giác BMN (g-g)
=> BA/BM=BC/BN=> BN=BM.BC/BA=18.20/12=30cm
b) tam giác PAN vuong tại A và tam giác PMC vuong tại M có
góc APN=góc MPC (đối đỉnh)
=> tam giác PAN đồng dạng tam giác PMC (g-g)
=> PA/PM=PN/PC
=> PA.PC=PM.PN (đpcm)
c) xét tam giác BNC có MN và AC là hai đường cao cắt nhau tại P
=> BP là đường cao thứ 3 kẻ từ B
=> BP vuong góc NC (đpcm)
10 tháng 1
a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có
\(\widehat{AEC}\) chung
Do đó: ΔEAC đồng dạng với ΔEDB
b: Ta có: ΔEDB vuông tại D
=>\(\widehat{DEB}+\widehat{DBE}=90^0\)
=>\(\widehat{DEB}=60^0\)
Xét ΔEDB vuông tại D có \(cosE=\dfrac{ED}{EB}\)
=>\(\dfrac{ED}{EB}=cos60=\dfrac{1}{2}\)
Ta có: ΔEAC đồng dạng với ΔEDB
=>\(\dfrac{EA}{ED}=\dfrac{EC}{EB}\)
=>\(\dfrac{EA}{EC}=\dfrac{ED}{EB}\)
Xét ΔEAD và ΔECB có
EA/EC=ED/EB
góc E chung
Do đó: ΔEAD đồng dạng với ΔECB
=>\(\dfrac{S_{EAD}}{S_{ECB}}=\left(\dfrac{ED}{EB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ECB}=50\cdot4=200\left(cm^2\right)\)
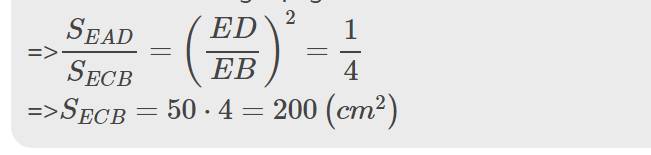
a: Xét ΔBMN vuông tại N và ΔBCA vuông tại A có
góc B chung
=>ΔBMN đồng dạng với ΔBCA
b: ΔBMN đồng dạng với ΔBCA
=>BM/BC=BN/BA
=>BM*BA=BN*BC