cho ch D A B E C cho hình vẽ trên và \(\frac{AD}{BD}=\frac{AE}{EC}\)cmr: \(\frac{AD}{AB}=\frac{AE}{EC}\)và...
Đọc tiếp
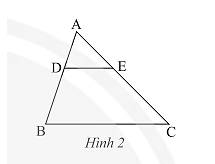
cho chcho hình vẽ trên và \(\frac{AD}{BD}=\frac{AE}{EC}\)cmr: \(\frac{AD}{AB}=\frac{AE}{EC}\)và DB.AC=CE.AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
DT
14 tháng 2 2020
a) Theo bài ra ta có:\(\frac{AE}{EC}=\frac{3}{4}\)=> \(\frac{AE}{EC+AE}=\frac{3}{4+3}\Rightarrow\frac{AE}{AC}=\frac{3}{7}\)
Xét ΔABC có DE//BC => \(\frac{DE}{BC}=\frac{AE}{AC}=\frac{3}{7}\) (hệ quả đ/lí Ta-lét)
=> DE = \(\frac{3}{7}BC=\frac{3}{7}.28=12\left(cm\right)\)
b) Xét ΔABC có DE//BC => \(\frac{AD}{BD}=\frac{AE}{EC}\) (đ/lí Ta-lét)
Mà \(\frac{AD}{BD}=\frac{EC}{AE}\left(gt\right)\) => \(\frac{AE}{EC}=\frac{EC}{AE}\) (=\(\frac{AD}{BD}\))
=>AE2=EC2 => AE = EC
=> E là trung điểm của AC.
Xét ΔABC có: DE//BC ; E là trung điểm của AC (cmt)
=> D là trung điểm của AB
Chúc bạn học tốt!
26 tháng 6 2023
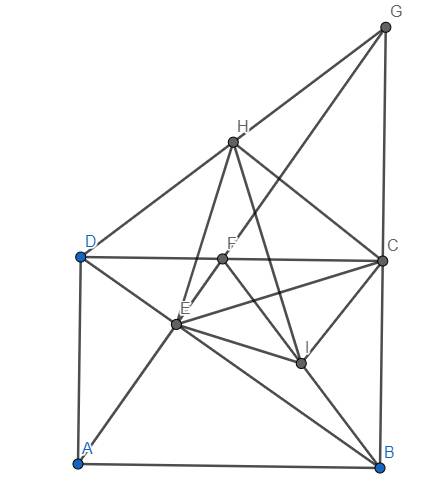
a) Ý 1: Dựa vào \(\widehat{AEB}=\widehat{DAB}=90^o\) và \(\widehat{ABD}\) chung, suy ra \(\Delta ABE~\Delta DBA\left(g.g\right)\)
Ý 2: Từ \(\Delta ABE~\Delta DBA\Rightarrow\dfrac{AB}{BD}=\dfrac{BE}{AB}\Rightarrow AB^2=BE.BD\)
b) Dễ thấy \(\widehat{DEF}=\widehat{BEG}=90^o\) và \(\widehat{DFE}=\widehat{EBG}\) (vì cùng phụ với \(\widehat{BDC}\)) nên suy ra \(\Delta EDF~\Delta EGB\left(g.g\right)\) \(\Rightarrow\dfrac{ED}{EG}=\dfrac{EF}{EB}\) \(\Rightarrow EG.EF=ED.EB\) (1)
Mặt khác, dễ dàng cm \(\Delta EAD~\Delta EBA\left(g.g\right)\) \(\Rightarrow\dfrac{EA}{EB}=\dfrac{ED}{EA}\) \(\Rightarrow EA^2=EB.ED\) (2)
Từ (1) và (2) \(\Rightarrow EA^2=EG.EF\left(=EB.ED\right)\)
c) Dễ thấy F là trực tâm của \(\Delta GBD\). \(\Delta GED\) vuông tại E có trung tuyến EH nên \(EH=\dfrac{1}{2}DG\). Tương tự suy ra \(CH=\dfrac{1}{2}DG\). Từ đó \(EH=DH\). Suy ra H nằm trên đường trung trực của đoạn CE (3)
Mặt khác, \(\Delta EBF\) vuông tại E có trung tuyến EI nên \(EI=\dfrac{1}{2}BF\). Tương tự, ta có \(CI=\dfrac{1}{2}BF\). Do đó \(EI=CI\) hay I nằm trên đường trung trực của đoạn CE (4)
Từ (3) và (4), suy ra HI là đường trung trực của đoạn CE, suy ra \(HI\perp CE\) (đpcm)
13 tháng 8 2017
Ta nối E với D :
Ta có hình như sau :
ta thấy hình tam giác ADC =\(\frac{1}{2}\)DEAC
\(\Leftrightarrow\)ADE =\(\frac{1}{2}\)DEAC
\(\Rightarrow\)ADE = ADC
Mà đoạn AD = EC = \(\frac{1}{3}\)
\(\Rightarrow\)AE = DC
\(\Rightarrow\)Tam giác AID = Tam giác CIE
24 tháng 5 2020
(Bạn Vẽ hình nhé)
Coi S là diện tích
Ta có : AID = 1/3 SABI ( chung chiều cao hạ từ đỉnh I xuống đáy AB , AD = 1/3 AI)
SCIE = 1/3 SBIC (chung chiều cao hạ từ đỉnh I xuống đáy BC, EC = 1/3 BC)
Ta thấy: SAID = SCIE vì SAID = SCIE= 1/3
Vậy kết luận SAID = SCIE
(k vào đúng nếu các bạn thấy hợp lí , k vào sai nếu các bạn thấy thiếu hoặc sai nhé)